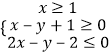题目内容
【题目】已知函数f(x)= ![]() .
.
(1)求f(x)的极值;
(2)试比较20162017与20172016的大小,并说明理由.
【答案】
(1)解:f(x)= ![]() 的定义域是(0,+∞),
的定义域是(0,+∞),
f′(x)= ![]() =
= ![]() ,
,
令f′(x)>0,解得:x<e,令f′(x)<0,解得:x>e,
∴f(x)在(0,e)递增,在(e,+∞)递减,
∴f(x)极大值=f(e)= ![]() ,无极小值;
,无极小值;
(2)解:∵f(x)在( ![]() ,+∞)递减,
,+∞)递减,
∴ ![]() >
> ![]() ,
,
∴2017ln2016>2016ln2017,
∴20162017>20172016.
【解析】(1)求出f(x)的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可;(2)根据函数的单调性判断即可.
【考点精析】解答此题的关键在于理解函数的极值与导数的相关知识,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问部分职工,根据被访问职工对该部门的评分,绘制频率分布直方图(如图所示).
(1)求频率分布表中①、②、③位置相应数据,并在答题纸上完成频率分布直方图;
组号 | 分组 | 频数 | 频率 |
第1组 | [50,60) | 5 | 0.050 |
第2组 | [60,70) | ① | 0.350 |
第3组 | [70,80) | 30 | ② |
第4组 | [80,90) | 20 | 0.200 |
第5组 | [90,100] | 10 | 0.100 |
合计 | ③ | 1.00 | |
(2)为进一步了解情况,该企业决定在第3,4,5组中用分层抽样抽取5名职工进行座谈,求第3,4,5组中各自抽取的人数;
(3)求该样本平均数 ![]() .
.