Question

【题目】已知函数y=f（x），若在定义域内存在x0 ， 使得f（﹣x0）=﹣f（x0）成立，则称x0为函数y=f（x）的局部对称点．
（1）若a、b∈R且a≠0，证明：函数f（x）=ax2+bx﹣a必有局部对称点；
（2）若函数f（x）=2x+c在定义域[﹣1，2]内有局部对称点，求实数c的取值范围；
（3）若函数f（x）=4x﹣m2x+1+m2﹣3在R上有局部对称点，求实数m的取值范围．

Answer 1

【答案】
（1）证明：由f（x）=ax2+bx﹣a得f（﹣x）=ax2﹣bx﹣a

代入f（﹣x）+f（x）=0得，（ax2+bx﹣a）+（ax2﹣bx﹣a）=0，

得到关于x的方程ax2﹣a=0（a≠0），

其中△=4a2，由于a∈R且a≠0，所以△＞0恒成立

所以函数f（x）=ax2+bx﹣a（a≠0）必有局部对称点

（2）证明：方程2x+2﹣x+2c=0在区间[﹣1，2]上有解，于是﹣2c=2x+2﹣x

设t=2x（﹣1≤x≤2）， ， 其中

所以

（3）证明：f（﹣x）=4﹣x﹣m2﹣x+1+m2﹣3，

由于f（﹣x）+f（x）=0，所以4﹣x﹣m2﹣x+1+m2﹣3=﹣（4x﹣m2x+1+m2﹣3）

于是（4x+4﹣x）﹣2m（2x+2﹣x）+2（m2﹣3）=0（*）在R上有解

令2x+2﹣x=t（t≥2），则4x+4﹣x=t2﹣2，

所以方程（*）变为t2﹣2mt+2m2﹣8=0在区间[2，+∞）内有解，需满足条件：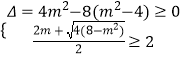

即 ，

化简得

【解析】（1）根据局部对称点的定义，结合已知中二次函数的图象和性质，可证明得结论；（2）若函数f（x）=2x+c在定义域[﹣1，2]内有局部对称点，则方程2x+2﹣x+2c=0在区间[﹣1，2]上有解，解得实数c的取值范围；（3）若函数f（x）=4x﹣m2x+1+m2﹣3在R上有局部对称点，则方程（4x+4﹣x）﹣2m（2x+2﹣x）+2（m2﹣3）=0（*）在R上有解，解得实数m的取值范围．
【考点精析】本题主要考查了二次函数的性质的相关知识点，需要掌握当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减才能正确解答此题．