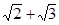题目内容
已知三棱锥O-ABC中,OA、OB、OC两两互相垂直,OC=1,OA=x, OB=y,若x+y=4,则已知三棱锥O-ABC体积的最大值是 .
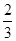
解:∵x>0,y>0且x+y=4,
由基本不等式得:
xy≤[(x+y )/2 ]2=4
又∵OA、OB、OC两两互相垂直,OC=1,
∴三棱锥O-ABC体积V="1" /3 ×1 /2 ×OA×OB×OC="1" /6 xy≤2/ 3即三棱锥O-ABC体积的最大值是2/ 3
故答案为:2 3
由基本不等式得:
xy≤[(x+y )/2 ]2=4
又∵OA、OB、OC两两互相垂直,OC=1,
∴三棱锥O-ABC体积V="1" /3 ×1 /2 ×OA×OB×OC="1" /6 xy≤2/ 3即三棱锥O-ABC体积的最大值是2/ 3
故答案为:2 3

练习册系列答案
相关题目
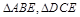 折起,使得B与C重合于O.
折起,使得B与C重合于O. AO;
AO;
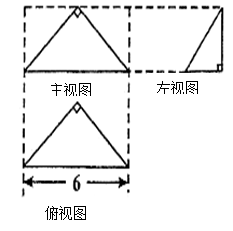
 ,侧棱长为
,侧棱长为 的正六棱柱的所有顶点都在一个球面上,则此球的体积为 .
的正六棱柱的所有顶点都在一个球面上,则此球的体积为 . ,那么这个三棱锥的体积是
,那么这个三棱锥的体积是 

 中,侧棱
中,侧棱 底面
底面 ,
,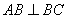 ,
, 为
为 的中点,
的中点,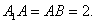

 平面
平面 ;
; 作
作 于点
于点 ,求证:直线
,求证:直线 平面
平面
 的体积为3,求
的体积为3,求 的长度
的长度 ,且它的8个顶点都在同一个球面上,这个球面的表面积为125π 则该球的半径为( )
,且它的8个顶点都在同一个球面上,这个球面的表面积为125π 则该球的半径为( )


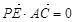 ,则动点P的轨迹的周长为( )
,则动点P的轨迹的周长为( )