题目内容
13.已知函数f(x)=-3x2+a(5-a)x+b,a,b∈R.(1)若不等式f(x)>0的解集为(-1,3),求实数a,b的值;
(2)若b为常数,解关于a的不等式f(1)<0.
分析 (1)根据题意并结合一元二次不等式与一元二方程的关系,可得方程-3x2+a(5-a)x+b=0的两根分别为-1和3,由此建立关于a、b的方程组并解之,即可得到实数a、b的值;
(2)由f(1)<0.得a2-5a-b+3>0,根据△与0的关系,加以讨论,即可得到答案.
解答 (1)由题意知,-1和3是方程-3x2+a(5-a)x+b=0的两个根,…(3分)
∴$\left\{\begin{array}{l}{3+d(5-a)-b=0}\\{27-3a(5-a)-b=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=2}\\{b=9}\end{array}\right.$或$\left\{\begin{array}{l}{a=3}\\{b=9}\end{array}\right.$.…(6分)
(2)由f(1)<0,得a2-5a-b+3>0,
△=(-5)2-4(-b+3)=13+4b,…(8分)
10当△<0即b<-$\frac{13}{4}$时,a∈R,…(10分)
20当△=0即b=-$\frac{13}{4}$时,解集为{a|a≠$\frac{5}{2}$,a∈R}} …(12分)
30当△>0即b>-$\frac{13}{4}$时,解集为{a>$\frac{5+\sqrt{4b+13}}{2}$,或a<$\frac{5-\sqrt{4b+13}}{2}$}} …(14分)
点评 本题给出二次函数,讨论不等式不等式f(x)>0的解集并求参数的值,着重考查了一元二次不等式的应用、一元二次不等式与一元二方程的关系等知识,属于中档题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知复数z=$\frac{2i}{1+i}$,则复数z的共轭复数$\overline{z}$是( )
| A. | -1+i | B. | -1-i | C. | 1-i | D. | 1+i |
18.已知定义域为R的奇函数f(x)的导数为f′(x),当x≠0时,f′(x)+$\frac{f(x)}{x}$>0,若a=f(1),b=-2f(-2),c=ln3f(ln3),则下列关于a,b,c的大小关系正确的是( )
| A. | a>b>c | B. | c>a>b | C. | c>b>a | D. | b>c>a |
2.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x,x>0}\\{{2}^{x},x≤0}\end{array}\right.$,若f(a)=$\frac{1}{4}$,则a的值为( )
| A. | -2或$\frac{1}{4}$ | B. | $\root{4}{2}或-2$ | C. | -2 | D. | $\root{4}{2}$ |
3.执行如图所示的程序框图,若输出的结果是27,则输入的数是( )
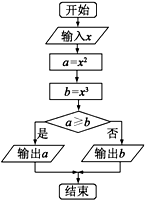

| A. | -3或-3$\sqrt{3}$ | B. | 3或-3$\sqrt{3}$ | C. | -3或3$\sqrt{3}$ | D. | 3或3$\sqrt{3}$ |