题目内容
8.数列$\frac{3}{2},\frac{5}{3},\frac{7}{4},\frac{9}{5}$,…的一个通项公式为an=$\frac{2n+1}{n+1}$.分析 根据题意,分析数列的各项的分母与分母的变化规律,进而用含有n的式子表示出来,即可得答案.
解答 解:根据题意,所给数列的各项分母依次为2、3、4、5…,为n+1,
而各项的分子依次为3、5、7、9…,为2n+2,
则各项可以用$\frac{2n+1}{n+1}$表示,即一个通项公式为$\frac{2n+1}{n+1}$,
故答案为:$\frac{2n+1}{n+1}$.
点评 本题考查数列的表示与归纳推理的运用,解答的关键在于根据所给的数列的特点,发现数列的变化规律.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.二项式${(x-\frac{2}{x})}^{6}$的展开式中各项系数和是( )
| A. | 1 | B. | 0 | C. | -1 | D. | 2 |
19.直线ax+by+c=0与圆x2+y2=9相交于两点M、N,若c2=a2+b2,则|MN|=( )
| A. | 4$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{10}$ | D. | $\sqrt{10}$ |
3.将4位同学分到三个不同的班级,每个班级至少有一位同学,则不同的分法有( )
| A. | 34种 | B. | 72种 | C. | 64种 | D. | 36种 |
20.已知角α的终边经过点$P({-1,-\sqrt{3}})$,则tanα等于( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | -$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | -$\frac{1}{2}$ |
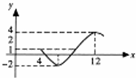 +c(A>0,ω>0,φ>0)图象的一部分.
+c(A>0,ω>0,φ>0)图象的一部分.