题目内容
18.已知定义域为R的奇函数f(x)的导数为f′(x),当x≠0时,f′(x)+$\frac{f(x)}{x}$>0,若a=f(1),b=-2f(-2),c=ln3f(ln3),则下列关于a,b,c的大小关系正确的是( )| A. | a>b>c | B. | c>a>b | C. | c>b>a | D. | b>c>a |
分析 令g(x)=xf(x),则g′(x)=f(x)+xf′(x).由于当x≠0时,f′(x)+$\frac{f(x)}{x}$>0,可得:当x>0时,xf′(x)+f(x)>0.即当x>0时,g′(x)>0,因此当x>0时,函数g(x)单调递增.即可得出.
解答 解:令g(x)=xf(x),则g′(x)=f(x)+xf′(x).
∵当x≠0时,f′(x)+$\frac{f(x)}{x}$>0,
∴当x>0时,xf′(x)+f(x)>0.
即当x>0时,g′(x)>0,
因此当x>0时,函数g(x)单调递增.
∵函数f(x)为奇函数,g(x)=xf(x)是偶函数
∴b=-2f(-2)=2f(2),
∵1<ln3<2,
∴g(2)>g(ln3)>g(1),即b>c>a,
故选:D.
点评 本题考查了通过构造函数利用导数研究函数的单调性比较大小,考查了推理能力,属于中档题.

练习册系列答案
相关题目
9.下列算法语句的处理功能是( )
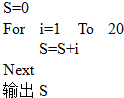
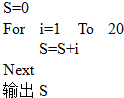
| A. | S=1+2+3+…+20 | B. | S=1+2+3+…+19 | C. | S=2+3+…+20 | D. | S=2+3+…+19 |
3.已知$\vec a$、$\vec b$为两个单位向量,则一定有( )
| A. | $\vec a$=$\vec b$ | B. | $\vec a•\vec b=0$ | C. | $\vec a•\vec b=1$ | D. | $\vec a•\vec a=\vec b•\vec b$ |