题目内容
【题目】(1)设![]() 是给定实数,解关于
是给定实数,解关于![]() 的不等式
的不等式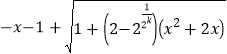
![]() ;
;
(2)设![]() 是一个给定实数,试求出1中
是一个给定实数,试求出1中![]() 的取值范围,使得不等式
的取值范围,使得不等式![]() 能满足1中的式子。
能满足1中的式子。
【答案】(1)见解析;(2)见解析
【解析】
(1)原不等式


下面对![]() 的取值分三种情形讨论:
的取值分三种情形讨论:
ⅰ.若![]() ,则式①变为
,则式①变为![]() ,即
,即![]() .
.
ⅱ.若![]() ,则
,则![]() ,显然
,显然![]() 满足式①.
满足式①.
下设![]() ,则式①
,则式①





![]()
 .
.
故当![]() 时,原不等式的解为
时,原不等式的解为 .
.
综合ⅰ、ⅱ知,当![]() 时,原不等式的解为
时,原不等式的解为 .
.
ⅲ.若![]() ,则
,则![]() .
.
式①左边的定义域为



下面再考虑式①的右边, 分成三种情形:
a.若![]() ,即
,即![]() ,亦即
,亦即![]() ,此时,显然
,此时,显然![]() 满足式①.
满足式①.
下设![]() ,则式①
,则式①
 。
。
(过程同ⅱ完全一样)所以,当![]() 时,原不等式的解为
时,原不等式的解为

 ,
,
又当![]() 时,有
时,有

![]()
 ,显然成立.
,显然成立.
因此,当![]() 时,原不等式的解为
时,原不等式的解为
 。
。
b.若![]() ,即
,即![]() ,此时,式①的右边为0,则由式②得,当
,此时,式①的右边为0,则由式②得,当![]() 时,原不等式的解为
时,原不等式的解为
 ,
,
即![]()
c.若![]() ,即
,即![]() ,此时,
,此时,![]() 满足式①(因为式①的右边小于0)
满足式①(因为式①的右边小于0)
下设![]() ,即
,即![]() ,此时,式①的右边大于或等于0,则式①
,此时,式①的右边大于或等于0,则式①

 .
.
故当![]() 时,原不等式的解恰好是式②.
时,原不等式的解恰好是式②.
(2)由1的结论可知,当![]() 时,都不合题目要求,只须考虑
时,都不合题目要求,只须考虑![]() 。
。
当![]() 时,令
时,令![]() ,显然
,显然![]() 。
。
由1的结论得
![]() ,
,
即![]()
下面对![]() 分两种情形讨论。
分两种情形讨论。
ⅰ.当![]() ,即
,即![]() 时,式③显然成立,故当
时,式③显然成立,故当![]() 时,
时,![]() 符合题目要求。
符合题目要求。
ⅱ.当![]() ,即
,即![]() 时,式③
时,式③
![]()
a.若![]() ,即
,即![]() ,
,
则式④显然成立,故当
![]() 时,
时,![]() 符合题目要求
符合题目要求
b.若![]() ,即
,即![]() ,则式④
,则式④![]()
![]()
![]()
![]()
![]() .
.
令![]() .
.
易知![]() 是
是![]() 的增函数,
的增函数,![]() 的解为
的解为![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
【题目】根据以往的经验,某工程施工期间的降水量![]() (单位:
(单位:![]() )对工期的影响如下表:
)对工期的影响如下表:
降水量 |
|
|
|
|
工期延误天数 |
|
|
|
|
历年气象资料表明,该工程施工期间降水量![]() 小于
小于![]() 、
、![]() 、
、![]() 的概率分别为
的概率分别为![]() 、
、![]() 、
、![]() ,求:
,求:
(1)在降水量![]() 至少是
至少是![]() 的条件下,工期延误不超过
的条件下,工期延误不超过![]() 天的概率;
天的概率;
(2)工期延误天数![]() 的均值与方差.
的均值与方差.