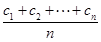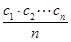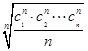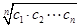题目内容
设等差数列{an}的前n项和为Sn,已知(a4-1)3+2 013(a4-1)=1,(a2 010-1)3+2 013(a2 010-1)=-1,则下列结论中正确的是( )
| A.S2 013=2 013,a2 010<a4 |
| B.S2 013=2 013,a2 010>a4 |
| C.S2 013=2 012,a2 010≤a4 |
| D.S2 013=2 012,a2 010≥a4 |
A
设f(x)=x3+2 013x,显然f(x)为奇函数和增函数,由已知得f(a4-1)=-f(a2 010-1),所以f(a4-1)=f(-a2 010+1),a4-1=-a2 010+1,a4+a2 010=2,S2 013=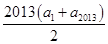 =2 013;显然1>-1,即f(a4-1)>f(a2 010-1),又f(x)为增函数,
=2 013;显然1>-1,即f(a4-1)>f(a2 010-1),又f(x)为增函数,
故a4-1>a2 010-1,即a4>a2 010.
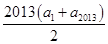 =2 013;显然1>-1,即f(a4-1)>f(a2 010-1),又f(x)为增函数,
=2 013;显然1>-1,即f(a4-1)>f(a2 010-1),又f(x)为增函数,故a4-1>a2 010-1,即a4>a2 010.

练习册系列答案
相关题目
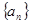 是等差数列,且
是等差数列,且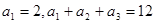
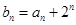 ,求数列
,求数列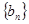 前n项和
前n项和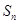
 的前n项和Tn=________.
的前n项和Tn=________.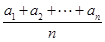 也为等差数列.类比这一性质可知,若正项数列{cn}是等比数列,且{dn}也是等比数列,则dn的表达式应为( )
也为等差数列.类比这一性质可知,若正项数列{cn}是等比数列,且{dn}也是等比数列,则dn的表达式应为( )