题目内容
【题目】已知函数f（x）=xlnx+2，g（x）=x2﹣mx．
（Ⅰ）求函数f（x）在[t，t+2]（t＞0）上的最小值；
（Ⅱ）若方程f（x）+g（x）=0有两个不同的实数根，求证：f（1）+g（1）＜0；
（Ⅲ）若存在x0∈[ 
，e]使得mf′（x）+g（x）≥2x+m成立，求实数m的取值范围．
【答案】解：（Ⅰ）f′（x）=lnx+1， 令f′（x）＞0，解得：x＞ 
，令f′（x）＜0，解得：0＜x＜ ，
∴f（x）在（0， ）递减，在（ ，+∞）递增，
若t≥ ，则f（x）在[t，t+2]递增，
∴f（x）min=f（t）=tlnt+2，
若0＜t＜ ，则f（x）在[t， ）递减，在（ ，t+2]递增，
∴f（x）min=f（ ）=2﹣ ；
（Ⅱ）若方程f（x）+g（x）=0有两个不同的实数根，
即m=lnx+x+ 
有两个不同的实数根，
令h（x）=lnx+x+ ，（x＞0），
即函数y=m和h（x）=lnx+x+ 有两个不同的交点，
而h′（x）= 
+1﹣ 
= 
，
令h′（x）＞0，解得：x＞1，令h′（x）＜0，解得：0＜x＜1，
故h（x）在（0，1）递减，在（1，+∞）递增，
故h（x）≥h（1）=3，
故m＞3，
故f（1）+g（1）=3﹣m＜0；
（Ⅲ）若存在x0∈[ ，e]使得mf′（x）+g（x）≥2x+m成立，
即存在x0∈[ ，e]使得m≤ 
成立，
令k（x）= 
，x∈[ ，e]，则k′（x）=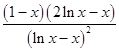 
，
易得2lnx﹣x＜0，
令k′（x）＞0，解得：x＞1，令k′（x）＜0，解得：x＜1，
故k（x）在[ ，1）递减，在（1，e]递增，
故k（x）的最大值是k（ ）或k（e），
而k（ ）= 
＜k（e）= 
，
故m≤ ．
【解析】（Ⅰ）求出函数的导数，解关于导函数的不等式，求出函数的单调区间，通过讨论t的范围，求出函数的最小值即可；（Ⅱ）问题转化为m=lnx+x+ 
有两个不同的实数根，令h（x）=lnx+x+ ，（x＞0），根据函数的单调性求出h（x）的最小值，求出m的范围，从而判断f（1）+g（1）的符号即可；（Ⅲ）问题转化为存在x0∈[ 
，e]使得m≤ 
成立，令k（x）= 
，x∈[ ，e]，根据函数的单调性求出m的范围即可．
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识点，需要掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减；求函数在
上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值
，
比较，其中最大的是一个最大值，最小的是最小值才能正确解答此题．
