题目内容
20.平面直角坐标系xOy中,过椭圆M:x2a2+y2b2=1x2a2+y2b2=1(a>b>0)过右焦点的直线x+y−√3=0x+y−√3=0交M于A,B两点,P为AB的中点,且OP的斜率为1212.(1)求椭圆M的方程;
(2)若C,D为椭圆M上的两点,且CD⊥AB,求|CD|的最大值.
分析 (1)把右焦点(c,0)代入直线可解得c.设A(x1,y1),B(x2,y2),线段AB的中点P(x0,y0),利用“点差法”即可得到a、b的关系式,再与a2=b2+c2联立即可得到a、b、c;
(2)由CD⊥AB可设直线CD的方程为y=x+t并与椭圆的方程联立得到根与系数的关系,进而可得到弦长|CD|的表达式,利用二次函数的单调性即可得到其最大值.
解答 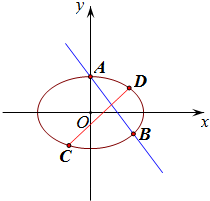 解:(1)把右焦点(c,0)代入直线x+y-√3√3=0,
解:(1)把右焦点(c,0)代入直线x+y-√3√3=0,
得c+0-√3√3=0,解得c=√3√3.
设A(x1,y1),B(x2,y2),线段AB的中点P(x0,y0),
则x12a2x12a2+y12b2y12b2=1,x22a2x22a2+y22b2y22b2=1,
两式相减得:x12−x22a2x12−x22a2+y12−y22b2y12−y22b2=0,
∴x1+x2a2x1+x2a2+y1+y2b2y1+y2b2×y1−y2x1−x2y1−y2x1−x2=0,
∴2x0a22x0a2+2y0b22y0b2×(-1)=0,
又∵kOP=1212=y0x0y0x0,∴1a21a2-12b212b2=0,即a2=2b2.
联立得{a2=2b2a2=b2+c2c=√3,解得{a2=6b2=3,
∴M的方程为:x26+y23=1;
(2)∵CD⊥AB,∴可设直线CD的方程为y=x+t,
联立直线CD与M的方程,消去y得:3x2+4tx+2t2-6=0,
∵直线CD与椭圆有两个不同的交点,
∴△=16t2-12(2t2-6)=72-8t2>0,解得:-3<t<3(*).
设C(x3,y3),D(x4,y4),∴x3+x4=-4t3,x3x4=2t2−63.
∴|CD|=√(1+12)[(x3+x4)2−4x3x4]
=√2[(−4t3)2−4×2t2−63]
=2√2•√18−2t23.
∴当且仅当t=0时,|CD|最大值为4,满足(*).
∴|CD|最大值为4.
点评 本题综合考查了椭圆的定义、标准方程及其性质、“点差法”、中点坐标公式、直线与椭圆相交问题转化为方程联立得到一元二次方程根与系数的关系、弦长公式、二次函数的单调性等基础知识,考查了推理能力、数形结合的思想方法、计算能力、分析问题和解决问题的能力,注意解题方法的积累,属于中档题.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案| A. | sinx | B. | -sinx | C. | cosx | D. | -cosx |
| A. | [0,113] | B. | [0,513] | C. | [113,1] | D. | [513,1] |
 如图,圆锥的顶点为P,底面圆为O,底面的一条直径为AB,C为半圆弧
如图,圆锥的顶点为P,底面圆为O,底面的一条直径为AB,C为半圆弧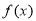 为奇函数,且当
为奇函数,且当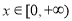 时,
时,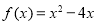 ,则
,则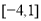 上的最大值为( )
上的最大值为( )