题目内容
14.设变量x,y满足约束条件$\left\{\begin{array}{l}{2x-y-7≥0}\\{x+y-8≥0}\\{x-2y-2≤0}\end{array}\right.$,则目标函数z=x2+y2的最小值为( )| A. | 32 | B. | 17 | C. | 40 | D. | 34 |
分析 作出不等式组对应的平面区域,利用z的几何意义进行求解即可.
解答  解:作出不等式组$\left\{\begin{array}{l}2x-y-7≥0\\ x+y-8≥0\\ x-2y-2≤0\end{array}\right.$对应的平面区域如图,
解:作出不等式组$\left\{\begin{array}{l}2x-y-7≥0\\ x+y-8≥0\\ x-2y-2≤0\end{array}\right.$对应的平面区域如图,
z的几何意义为区域内的点到原点的距离的平方,
由图象知:
OA的距离最小,
由$\left\{\begin{array}{l}2x-y-7=0\\ x+y-8=0\end{array}\right.$,解得$\left\{\begin{array}{l}x=5\\ y=3\end{array}\right.$,即A(5,3),
则|OA|2=52+32=34,
故z的最小值为d2=34,
故选:D.
点评 本题主要考查线性规划的应用以及两点间的距离公式的应用,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
9.设f0(x)=sinx,fn(x)=fn-1′(x),n∈N+,则f2010(x)=( )
| A. | sinx | B. | -sinx | C. | cosx | D. | -cosx |
19.已知F1,F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两个焦点,P是C上一点,若|PF1|•|PF2|=8a2,且△PF1F2的最小内角为30°,则双曲线C的离心率是( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
6.如图是一个几何体的三视图,则这个几何体的体积为( )
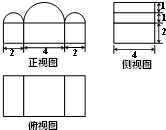

| A. | 16+3π | B. | 32+6π | C. | 64+12π | D. | 64+6π |
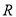 的函数
的函数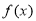 满足:
满足: .若
.若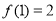 ,则
,则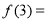 ________.
________. 十八世纪,法国数学家布丰和勒可莱尔提出投针问题:在平面上画有一组间距为a的平行线,将一根长度为l的针任意掷在这个平面上,求得此针与平行线中任一条相交的概率p=$\frac{2l}{πa}$(π为圆周率).已知l=3.14,a=6,π≈3.14,现随机掷14根相同的针(长度为l)在这个平面上,记这些针与平行线(间距为a)相交的根数为m,其相应的概率为p(m).当p(m)取得最大值时,m=4或5.
十八世纪,法国数学家布丰和勒可莱尔提出投针问题:在平面上画有一组间距为a的平行线,将一根长度为l的针任意掷在这个平面上,求得此针与平行线中任一条相交的概率p=$\frac{2l}{πa}$(π为圆周率).已知l=3.14,a=6,π≈3.14,现随机掷14根相同的针(长度为l)在这个平面上,记这些针与平行线(间距为a)相交的根数为m,其相应的概率为p(m).当p(m)取得最大值时,m=4或5.