题目内容
4. 若双曲线$\frac{{x}^{2}}{8}$-y2=1过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,且它们的离心率互为倒数.
若双曲线$\frac{{x}^{2}}{8}$-y2=1过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,且它们的离心率互为倒数.(I)求椭圆C的标准方程;
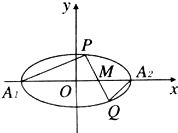
(Ⅱ)如图,椭圆C的左、右顶点分别为A1,A2点M(1,0)的直线l与椭圆C交于P、Q两点,设直线A1P与A2Q的斜率别为k1,k2试问,是否存在实数m,使得k1+mk2=0?若存在,求m的值;若不存在,请说明理由.
分析 (Ⅰ)求得双曲线的离心率,由题意可得椭圆的离心率,代入椭圆的焦点,可得c,再由离心率公式和a,b,c的关系,即可得到椭圆方程;
(Ⅱ)假设存在实数m,使得k1+mk2=0.讨论直线l的斜率不存在和存在,设出直线方程,代入椭圆方程,运用韦达定理和直线的斜率公式,化简整理,即可得到m的值,进而判断存在.
解答 解:(Ⅰ)双曲线$\frac{{x}^{2}}{8}$-y2=1的离心率为$\frac{\sqrt{8+1}}{\sqrt{8}}$=$\frac{3}{2\sqrt{2}}$,
它们的离心率互为倒数,可得椭圆的离心率为e=$\frac{c}{a}$=$\frac{2\sqrt{2}}{3}$,
由题意可得c2=8,即c=2$\sqrt{2}$,则a=3,b=1,
则有椭圆方程为$\frac{{x}^{2}}{9}$+y2=1;
(Ⅱ)假设存在实数m,使得k1+mk2=0.
当直线l的斜率不存在时,P(1,$\frac{2\sqrt{2}}{3}$),Q(1,-$\frac{2\sqrt{2}}{3}$),A1(-3,0),A2(3,0),
则k1=$\frac{\frac{2\sqrt{2}}{3}}{1+3}$=$\frac{\sqrt{2}}{6}$,k2=$\frac{-\frac{2\sqrt{2}}{3}}{1-3}$=$\frac{\sqrt{2}}{3}$,则m=-$\frac{{k}_{1}}{{k}_{2}}$=-$\frac{1}{2}$;
当直线l的斜率存在时,设P(x1,y1),Q(x2,y2),
直线l:y=k(x-1),代入椭圆方程可得,
(1+9k2)x2-18k2x+9k2-9=0,
x1+x2=$\frac{18{k}^{2}}{1+9{k}^{2}}$,x1x2=$\frac{9{k}^{2}-9}{1+9{k}^{2}}$,
则m=-$\frac{{k}_{1}}{{k}_{2}}$=-$\frac{\frac{{y}_{1}}{{x}_{1}+3}}{\frac{{y}_{2}}{{x}_{2}-3}}$=-$\frac{k({x}_{1}-1)({x}_{2}-3)}{k({x}_{1}+3)({x}_{2}-1)}$=-$\frac{{x}_{1}{x}_{2}-3({x}_{1}+{x}_{2})+2{x}_{2}+3}{{x}_{1}{x}_{2}-({x}_{1}+{x}_{2})+4{x}_{2}-3}$
=-$\frac{9{k}^{2}-9-3•18{k}^{2}+2(1+9{k}^{2}){x}_{2}+3(1+9{k}^{2})}{9{k}^{2}-9-18{k}^{2}+4(1+9{k}^{2}){x}_{2}-3(1+9{k}^{2})}$
=-$\frac{2(1+9{k}^{2}){x}_{2}-18{k}^{2}-6}{4(1+9{k}^{2}){x}_{2}-36{k}^{2}-12}$=-$\frac{1}{2}$,
故存在m=-$\frac{1}{2}$,满足题意.
点评 本题考查椭圆的方程和性质,主要考查椭圆的离心率和方程的运用,联立直线方程,运用韦达定理,考查直线的斜率公式和化简整理的运算求解能力,属于中档题.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案| A. | sinx | B. | -sinx | C. | cosx | D. | -cosx |
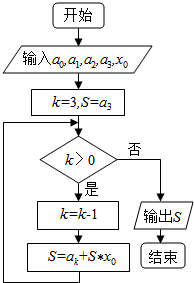
| A. | a1+x0(a3+x0(a0+a2x0))的值 | B. | a3+x0(a2+x0(a1+a0x0))的值 | ||
| C. | a0+x0(a1+x0(a2+a3x0))的值 | D. | a2+x0(a0+x0(a3+a1x0))的值 |
| A. | c<a<b | B. | b<c<a | C. | a<b<c | D. | b<a<c |
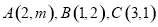 ,若
,若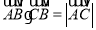 ,则实数
,则实数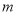 等于( )
等于( )
