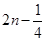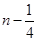题目内容
已知函数 ,则
,则 ,
,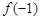 ,
, 的大小关系为
的大小关系为
A.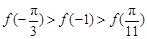 | B.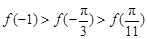 |
C. | D. |
A
解析试题分析:因为,f(-x)=-xsin(-x)=xsinx=f(x),所以,f(x)=xsinx为偶函数.
又f′(x)=sinx+xcosx,所以,当x∈(0,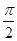 )时,sinx>0,cosx>0,f′(x)=sinx+xcosx>0,
)时,sinx>0,cosx>0,f′(x)=sinx+xcosx>0,
即f(x)在(0,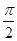 )上单调递增,所以
)上单调递增,所以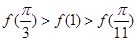 ,即
,即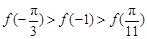 ,故选A。
,故选A。
考点:函数的奇偶性,应用导数研究函数的单调性。
点评:中档题,比较大小问题,往往应用函数的单调性,而研究函数的单调性,又常常利用导数。本题利用函数的奇偶性加以转化,是关键点之一。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设 是R上的偶函数,且在
是R上的偶函数,且在 上单调递增,则
上单调递增,则 ,
,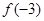 ,
, 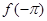 的大小顺序是:( )
的大小顺序是:( )
A.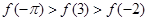 | B.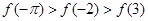 |
C.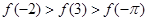 | D.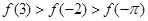 |
若a>l,设函数f(x)=ax+x -4的零点为m,函数g(x)= logax+x-4的零点为n,则 的最小值为
的最小值为
| A.1 | B.2 | C.4 | D.8 |
定义在 上的函数
上的函数 ,满足
,满足 ,
,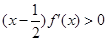 ,若
,若 且
且 ,则有( ).
,则有( ).
A. | B. | C. | D.不能确定 |
某大学的信息中心A与大学各部门、各院系B,C,D,E,F,G,H,I之间拟建立信息联网工程,实际测算的费用如图所示(单位:万元).请观察图形,可以不建部分网线,而使得中心与各部门、院系彼此都能连通(直接或中转),则最少的建网费用(万元)是( )
| A.12 | B.13 |
| C.14 | D.16 |
已知函数 的定义域为
的定义域为 ,则函数
,则函数 的定义域为( )
的定义域为( )
A. | B. | C. | D. |
若f(x)是R上周期为5的奇函数,且满足f(1)=1,f(2)=2,则f(3)-f(4)等于( )
| A.2 | B.1 | C.-2 | D.-1 |
 的图象的顶点在第四象限,则函数
的图象的顶点在第四象限,则函数 的图象是( ).
的图象是( ).

 是定义在
是定义在 上的偶函数,且对任意的
上的偶函数,且对任意的
 .当
.当 时,
时, .若直线
.若直线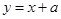 与函数
与函数 的图象有两个不同的公共点,则实数
的图象有两个不同的公共点,则实数 的值为( )
的值为( )