题目内容
若a>l,设函数f(x)=ax+x -4的零点为m,函数g(x)= logax+x-4的零点为n,则 的最小值为
的最小值为
| A.1 | B.2 | C.4 | D.8 |
A
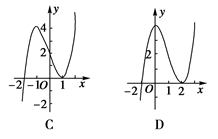
解析试题分析:作三个函数 的图像如下,由于函数f(x)=ax+x -4的零点为m,则
的图像如下,由于函数f(x)=ax+x -4的零点为m,则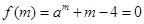 ,化为
,化为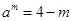 ,所以函数f(x)的零点m就是函数
,所以函数f(x)的零点m就是函数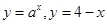 交点的横坐标。同理:函数g(x)的零点n就是
交点的横坐标。同理:函数g(x)的零点n就是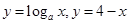 交点的横坐标。求得直线
交点的横坐标。求得直线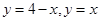 的交点为
的交点为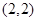 ,由于函数
,由于函数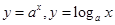 的图像关于
的图像关于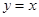 对称,则
对称,则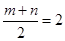 ,即
,即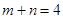 ,所以
,所以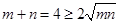 ,
,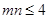 ,
,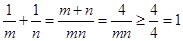 。故选A。
。故选A。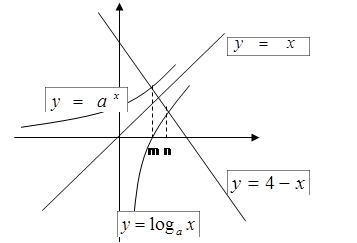
考点:函数的零点
点评:当函数的零点无法直接求出时,需通过画出函数的图像来求解。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知 是定义在R上的奇函数,若对于x≥0,都有f(x+2)=
是定义在R上的奇函数,若对于x≥0,都有f(x+2)= ,且
,且
当 时,
时, ,则
,则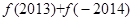 =( )
=( )
| A.1-e | B.e-1 | C.-l-e | D.e+l |
下列各组函数中,表示同一函数的是( )
A. | B. |
C. | D. |
函数 是定义在R上的奇函数,下列结论中,不正确的是
是定义在R上的奇函数,下列结论中,不正确的是
A. | B. |
C. | D. |
已知函数 ,则
,则 ,
,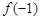 ,
, 的大小关系为
的大小关系为
A.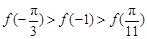 | B.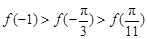 |
C. | D. |
下列函数中,不满足 的是( )
的是( )
A.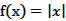 | B. | C. | D. |
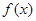 (
( R)满足
R)满足 ,
, ,则函数
,则函数 的图像是( )
的图像是( ) 



 的图象如图(1)所示(其中
的图象如图(1)所示(其中 是函数f(x)的导函数),下面四图象中,
是函数f(x)的导函数),下面四图象中,