题目内容
某大学的信息中心A与大学各部门、各院系B,C,D,E,F,G,H,I之间拟建立信息联网工程,实际测算的费用如图所示(单位:万元).请观察图形,可以不建部分网线,而使得中心与各部门、院系彼此都能连通(直接或中转),则最少的建网费用(万元)是( )
| A.12 | B.13 |
| C.14 | D.16 |
B
解析试题分析:根据题意可知可以不建部分网线而使得信息中心与各部门、各院系都能联通(直接或中转),从图形可以看出,最佳建网路线:A-H-G-F,A-E-D-C,A-B,A-I,最后计算出此时费用即可. 解:可以不建部分网线而使得信息中心与各部门、各院系都能联通(直接或中转),可考虑实际测算的费用每段中最小的网路线,最佳建网路线:A-H-G-F,A-E-D-C,A-B,A-I,此时费用为:1+1+1+1+2+2+3+2=13,故选B
考点:函数最值
点评:本题考查函数最值的应用,是一个读图题,从图形中观测出信息中心A与大学各部门,各院系B、C、D、E、F、G、H、I之间拟建立信息联网工程共有几条网路线,找一条包括实际测算的费用最小的网路线,是解题的关键,易错在未找到最佳建网路线.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
定义在 上的偶函数
上的偶函数 满足:对任意
满足:对任意 、
、
 (
(

 ),有
),有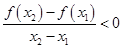 ,则( )
,则( )
A. |
B. |
C. |
D. |
函数f(x)=x2+2x-1 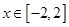 的值域为( )
的值域为( )
A.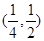 | B.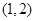 | C.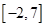 | D.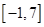 |
已知函数 ,则
,则 ,
,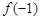 ,
, 的大小关系为
的大小关系为
A.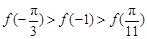 | B.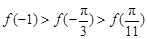 |
C. | D. |
把函数 的图像向左平移
的图像向左平移 个单位,所得曲线的一部分
个单位,所得曲线的一部分
如图示,则 的值分别为
的值分别为
A. | B. | C. | D. |
 的图象如图(1)所示(其中
的图象如图(1)所示(其中 是函数f(x)的导函数),下面四图象中,
是函数f(x)的导函数),下面四图象中,

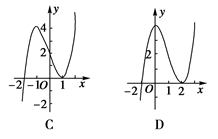



 的部分图象大致是( )
的部分图象大致是( )
 的图象大致是
的图象大致是