题目内容
【题目】某企业投入81万元经销某产品,经销时间共60个月,市场调研表明,该企业在经销这个产品期间第x个月的利润  (单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第x个月的当月利润率
(单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第x个月的当月利润率 ![]() ,例如:
,例如: ![]() .
.
(1)求g(10);
(2)求第x个月的当月利润率g(x);
(3)该企业经销此产品期间,哪个月的当月利润率最大,并求该月的当月利润率.
【答案】
(1)解:由题意得:f(1)=f(2)=f(3)=…═f(9)=f(10)=1
g(x)= ![]() =
= ![]() =
= ![]()
(2)解:当1≤x≤20时,f(1)=f(2)═f(x﹣1)=f(x)=1
∴g(x)= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
当21≤x≤60时,
g(x)= ![]()
= ![]()
= 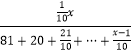
= 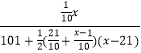
= 
∴当第x个月的当月利润率
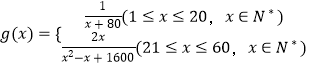
(3)解:当1≤x≤20时, ![]() 是减函数,
是减函数,
此时g(x)的最大值为 ![]()
当21≤x≤60时,
![]()
当且仅当 ![]() 时,即x=40时,
时,即x=40时,
![]() ,又∵
,又∵ ![]() ,
,
∴当x=40时, ![]()
所以,该企业经销此产品期间,第40个月的当月利润率最大,最大值为 ![]()
【解析】(1)当1≤x≤20时,f(x)=1,易知f(1)=f(2)=f(3)=…=f(9)=f(10)=1,从而知 ![]() (2)求第x个月的当月利润率,要考虑1≤x≤20,21≤x≤60时f(x)的值,代入
(2)求第x个月的当月利润率,要考虑1≤x≤20,21≤x≤60时f(x)的值,代入 ![]() 即可.(3)求那个月的当月利润率最大时,由(2)得出的分段函数,利用函数的单调性,基本不等式
即可.(3)求那个月的当月利润率最大时,由(2)得出的分段函数,利用函数的单调性,基本不等式 ![]() 可得,解答如下:
可得,解答如下:
【考点精析】关于本题考查的函数的最值及其几何意义,需要了解利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值才能得出正确答案.

练习册系列答案
相关题目