题目内容
【题目】已知 
=（2，﹣ 
）， 
=（sin2（ 
+x），cos2x）．令f（x）= ﹣1，x∈R，函数g（x）=f（x+φ），φ∈（0， 
）的图象关于（﹣ 
，0）对称． （Ⅰ） 求f（x）的解析式，并求φ的值；
（Ⅱ）在△ABC中sinC+cosC=1﹣ 
，求g（B）的取值范围．
【答案】解：（Ⅰ）∵f（x）= 
﹣1= 
=2 
， ∴ 
．
∴g（x）的图象的对称中心为 
．
又已知点（ 
）为g（x）的图象的一个对称中心，∴ 
．
而 
，∴ 
；
（Ⅱ）由 
得 
，
即 
，
∵ 
，
∴ 
．
两边平方得 
．
由 ，
得 
，∴ 
．
∴ 
， 
．
又 
，
又∵ 
，∴ 
，
∴ 
【解析】（Ⅰ）将函数进行化简，结合三角函数的图象和性质即可求函数f（x）的解析式，进一步求出图象的对称中心，即可得到φ的值；（Ⅱ）由已知条件化简得到sinC的值，求出C= 
，又 
，又 
，得到 
，即可求出g（B）的取值范围．
练习册系列答案
相关题目
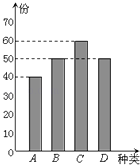
【题目】某学校餐厅新推出A、B、C、D四款套餐，某一天四款套餐销售情况的条形图如下．为了了解同学对新推出的四款套餐的评价，对每位同学都进行了问卷调查，然后用分层抽样的方法从调查问卷中抽取20份进行统计，统计结果如下面表格所示：
满意 | 一般 | 不满意 | |
A套餐 | 50% | 25% | 25% |
B套餐 | 80% | 0 | 20% |
C套餐 | 50% | 50% | 0 |
D套餐 | 40% | 20% | 40% |
（Ⅰ）若同学甲选择的是A款套餐，求甲的调查问卷被选中的概率；
（Ⅱ）若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈，求这两人中至少有一人选择的是D款套餐的概率．
