题目内容
9.函数$y=\frac{2x+4}{x-2},x∈[0,3]且x≠2$的值域为(-∞,-2]∪[10,+∞).分析 把函数恒等变形得出y=2+$\frac{8}{x-2}$,x∈[0,3]且x≠2,利用函数的单调性,结合不等式求解即可.
解答 解:∵函数$y=\frac{2x+4}{x-2},x∈[0,3]且x≠2$,
∴y=2+$\frac{8}{x-2}$,x∈[0,3]且x≠2,
∵-2≤x-2≤1,x-2≠0
∴$\frac{8}{x-2}$≤-4或$\frac{8}{x-2}$≥8
∴y≤-2或y≥10,
故答案为:(-∞,-2]∪[10,+∞)
点评 本题考查了分式函数的值域的求解,不等式的运用,是一道难度不大的题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知向量$\overrightarrow{a}$=(3,4),$\overrightarrow{b}$=(-3,1),$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,则tanθ等于( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | -3 | D. | 3 |
19.已知集合M={a,b,c},集合A={x|x⊆M},则集合A有几个元素( )
| A. | 3 | B. | 6 | C. | 7 | D. | 8 |
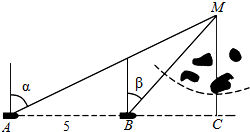 如图,一船由西向东航行,在A处测得某岛M的方位角为α,前进5km后到达B处,测得岛M的方位角为β.已知该岛周围3km内有暗礁,现该船继续东行.
如图,一船由西向东航行,在A处测得某岛M的方位角为α,前进5km后到达B处,测得岛M的方位角为β.已知该岛周围3km内有暗礁,现该船继续东行. 由曲线y=sinx,y=cosx与直线x=0,x=$\frac{π}{2}$所围成的平面图形(下图中的阴影部分)的面积是2$\sqrt{2}$-2.
由曲线y=sinx,y=cosx与直线x=0,x=$\frac{π}{2}$所围成的平面图形(下图中的阴影部分)的面积是2$\sqrt{2}$-2.