题目内容
光明中学准备组织学生去国家体育场“鸟巢”参观．参观期间，校车每天至少要运送544名学生．该中学后勤集团有7辆小巴、4辆大巴，其中小巴能载16人、大巴能载32人． 已知每辆客车每天往返次数小巴为5次、大巴为3次，每次运输成本小巴为48元，大巴为60元．请问每天应派出小巴、大巴各多少辆，能使总费用最少？
考点：简单线性规划
专题：计算题,应用题,作图题,不等式的解法及应用
分析：由题意设每天派出小巴x辆、大巴y辆，总运费为z元；则
，目标函数是z=240x+180y；利用线性规划求解．
|
解答：
解：设每天派出小巴x辆、大巴y辆，总运费为z元；
则
；
目标函数是z=240x+180y；
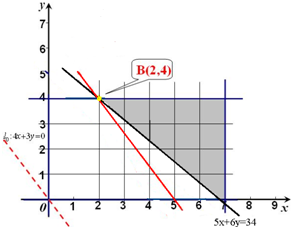
作平面区域如图，
由网格法可得：
x=2，y=4时，zmin=1200．
答：派4辆小巴、2辆大巴费用最少．
解：设每天派出小巴x辆、大巴y辆，总运费为z元；则
|
目标函数是z=240x+180y；
作平面区域如图，
由网格法可得：
x=2，y=4时，zmin=1200．
答：派4辆小巴、2辆大巴费用最少．
点评：本题考查了实际问题转化为数学问题的能力及线性规划的应用，属于中档题．
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
函数f（x）=
的零点是（ ）
| x3-x2 |
| x |
| A、-1 | B、0 | C、1 | D、0或-1 |
设a1，d为实数，首项为a1，公差为d的等差数列{an}的前n项的和为Sn，满足S5S6=-15，则a1的取值范围是（ ）
A、（-∞，-2
| ||||
B、[2
| ||||
C、（-∞，-2
| ||||
D、[2
|
在△ABC中，角A，B，C所对的边长分别为a，b，c，若∠C=120°，c=2a，则（ ）
| A、a＞b |
| B、a＜b |
| C、a=b |
| D、a与b的大小关系不能确定 |