题目内容
【题目】已知中心在坐标原点![]() 的椭圆
的椭圆![]() 经过点
经过点![]() ,且点
,且点![]() 为其右焦点.
为其右焦点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)是否存在平行于![]() 的直线
的直线![]() ,使得直线
,使得直线![]() 与椭圆
与椭圆![]() 有公共点,且直线
有公共点,且直线![]() 与
与![]() 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)不存在.
;(Ⅱ)不存在.
【解析】试题分析:(Ⅰ)设出椭圆的标准方程,利用椭圆的定义和焦点坐标求出有关参数值,进而得到椭圆的标准方程;(Ⅱ)先假设存在符合题意的直线![]() ,并设出直线方程,联立直线与椭圆的方程,得到关于
,并设出直线方程,联立直线与椭圆的方程,得到关于![]() 的一元二次方程,利用判别式为正和点到直线的距离公式进行求解.
的一元二次方程,利用判别式为正和点到直线的距离公式进行求解.
试题解析:(Ⅰ)依题意,可设椭圆![]() 的方程为
的方程为![]() ,且可知左焦点为
,且可知左焦点为![]() ,
,
从而有![]() ,解得
,解得![]() ,又
,又![]() ,∴
,∴![]() .
.
故椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)假设存在符合题意的直线![]() ,其方程为
,其方程为![]() .
.
由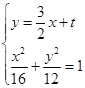 得
得![]() .
.
∵直线![]() 与椭圆
与椭圆![]() 有公共点,∴
有公共点,∴![]() ,解得
,解得![]() .
.
另一方面,直线![]() 与
与![]() 的距离等于4,可得
的距离等于4,可得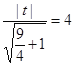 ,从而
,从而![]() .
.
由于![]() ,∴符合题意的直线
,∴符合题意的直线![]() 不存在.
不存在.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目