题目内容
【题目】如图,在平面直角坐标系xOy中,F1 , F2分别为椭圆 ![]() +
+ ![]() =1(a>b>0)的左、右焦点,顶点B的坐标为(0,b),连接BF2并延长交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连接F1C.
=1(a>b>0)的左、右焦点,顶点B的坐标为(0,b),连接BF2并延长交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连接F1C. 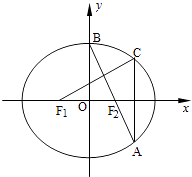
(1)若点C的坐标为( ![]() ,
, ![]() ),且BF2=
),且BF2= ![]() ,求椭圆的方程;
,求椭圆的方程;
(2)若F1C⊥AB,求椭圆离心率e的值.
【答案】
(1)解:∵C的坐标为( ![]() ,
, ![]() ),
),
∴ ![]() ,即
,即 ![]() ,
,
∵ ![]() ,
,
∴a2=( ![]() )2=2,即b2=1,
)2=2,即b2=1,
则椭圆的方程为 ![]() +y2=1
+y2=1
(2)解:设F1(﹣c,0),F2(c,0),
∵B(0,b),
∴直线BF2:y=﹣ ![]() x+b,代入椭圆方程
x+b,代入椭圆方程 ![]() +
+ ![]() =1(a>b>0)得(
=1(a>b>0)得( ![]() )x2﹣
)x2﹣ ![]() =0,
=0,
解得x=0,或x= ![]() ,
,
∵A( ![]() ,
, ![]() ),且A,C关于x轴对称,
),且A,C关于x轴对称,
∴C( ![]() ,﹣
,﹣ ![]() ),
),
则 ![]() =﹣
=﹣ ![]() =
= ![]() ,
,
∵F1C⊥AB,
∴ ![]() ×(
×( ![]() )=﹣1,
)=﹣1,
由b2=a2﹣c2得 ![]() ,
,
即e= ![]()
【解析】(1)根据椭圆的定义,建立方程关系即可求出a,b的值.(2)求出C的坐标,利用F1C⊥AB建立斜率之间的关系,解方程即可求出e的值.
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.

练习册系列答案
相关题目


