题目内容
19.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点为(3,0),直线x-y-1=0与双曲线右支相交于点P,则当双曲线离心率最小时的双曲线方程为$\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1.分析 由题意,$\frac{b}{a}$≥1,可得e=$\frac{c}{a}$≥$\sqrt{2}$,即可求出当双曲线离心率最小时,a=$\frac{3}{\sqrt{2}}$,可得b,即可得出结论.
解答 解:由题意,c=3,即有a2+b2=9,
当双曲线离心率最小时,直线y=x-1与双曲线相切,
联立直线方程和双曲线的方程,可得(b2-a2)x2+2a2x-a2-a2b2=0,
可得△=4a4+4(b2-a2)(a2+a2b2)=0,化为a2-b2=1,
解得a2=5,b2=4,
∴双曲线方程为$\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1.
故答案为:$\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1.
点评 本题考查双曲线的性质与方程,考查学生的计算能力,正确求出a,b是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.设数列{an}共有n项(n≥3,n∈N*),且a1=an=1,对于每个i(1≤i≤n-1,n∈N*)均有$\frac{{{a_{i+1}}}}{a_i}∈\{\frac{1}{5},1,5\}$.当n=10时,满足条件的所有数列{an}的个数为( )
| A. | 215 | B. | 512 | C. | 1393 | D. | 3139 |
14.假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:
若由资料知y对x呈线性相关关系.
(1)请画出上表数据的散点图;
(2)请根据最小二乘法求出线性回归方程$\widehat{y}$=bx+a的回归系数a,b;$b=\frac{\sum _{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum _{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}},a=\overline{y}-b\overline{x}$
(3)估计使用年限为10年时,维修费用是多少?
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)请画出上表数据的散点图;
(2)请根据最小二乘法求出线性回归方程$\widehat{y}$=bx+a的回归系数a,b;$b=\frac{\sum _{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum _{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}},a=\overline{y}-b\overline{x}$
(3)估计使用年限为10年时,维修费用是多少?
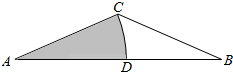 如图,在一个等腰三角形ABC内以A为圆心,腰AC长为半径画弧交底边AB于D,已知AC=1,∠A=30°,现向△ABC内任投一点,该点落在图中阴影部分的概率为$\frac{\sqrt{3}π}{9}$.
如图,在一个等腰三角形ABC内以A为圆心,腰AC长为半径画弧交底边AB于D,已知AC=1,∠A=30°,现向△ABC内任投一点,该点落在图中阴影部分的概率为$\frac{\sqrt{3}π}{9}$.