题目内容
【题目】已知![]() ,
,![]() ,直线
,直线![]() ,
,![]() ,
,![]() 与曲线
与曲线![]() 所围成的曲边梯形的面积为
所围成的曲边梯形的面积为![]() .其中
.其中![]() ,且
,且![]() .
.
(1)当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的值;
的值;
(2)请指出![]() ,
,![]() ,
,![]() 的大小,并且证明;
的大小,并且证明;
(3)求证:![]() .
.
【答案】(1)1;(2)![]() ,证明见解析;(3)见解析
,证明见解析;(3)见解析
【解析】
(1)构造函数![]() ,
,![]() 借助导数分析函数单调性,研究
借助导数分析函数单调性,研究![]() 的范围,即得解.
的范围,即得解.
(2)借助第(1)问的结论进行放缩,即得证;
(3)借助第(1)问的结论进行放缩和叠加,即得证;
(1)由已知得![]() 时,不合题意,所以
时,不合题意,所以![]() .
.
![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
令![]() ,
,![]() .
.
当![]() 时,
时,![]() 在
在![]() 上为增函数,此时
上为增函数,此时![]() 成立.
成立.
当![]() 时,
时,![]() 在
在![]() 上为减函数,不合题意,所以
上为减函数,不合题意,所以![]() .
.
令![]() ,
,![]() ,当
,当![]() 时,
时,![]() 在
在![]() 上为增函数,此时
上为增函数,此时![]() ,
,![]() 恒成立.
恒成立.
当![]() 时,
时,![]() 在
在![]() 上为减函数,不合题意,所以
上为减函数,不合题意,所以![]() .
.
综上得![]() .
.
(2)由(1)知![]() .令
.令![]() ,得
,得![]() ,
,
从而![]() ,
,
又因为![]() ,则
,则![]() .
.
(3)由已知![]()
![]()
![]() ,
,
因为![]() ,所以
,所以
![]()
![]() ,
,
![]()
![]() .
.
从而![]() .
.

【题目】一只红玲虫的产卵数![]() 和温度
和温度![]() 有关.现收集了7组观测数据如下表:
有关.现收集了7组观测数据如下表:
温度 | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
产卵数 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
为了预报一只红玲虫在![]() 时的产卵数,根据表中的数据建立了
时的产卵数,根据表中的数据建立了![]() 与
与![]() 的两个回归模型.模型①:先建立
的两个回归模型.模型①:先建立![]() 与
与![]() 的指数回归方程
的指数回归方程![]() ,然后通过对数变换
,然后通过对数变换![]() ,把指数关系变为
,把指数关系变为![]() 与
与![]() ;模型②:先建立
;模型②:先建立![]() 与
与![]() 的二次回归方程
的二次回归方程![]() ,然后通过变换
,然后通过变换![]() ,把二次关系变为
,把二次关系变为![]() 与
与![]() 的线性回归方程:
的线性回归方程:![]() .
.
(1)分别利用这两个模型,求一只红玲虫在![]() 时产卵数的预测值;
时产卵数的预测值;
(2)你认为用哪个模型得到的预测值更可靠?并说明理由.(参考数据:模型①的残差平方和![]() ,模型①的相关指数
,模型①的相关指数![]() ;模型②的残差平方和
;模型②的残差平方和![]() ,模型②的相关指数
,模型②的相关指数![]() ;
;![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在头胎生女孩家庭中抽取了5户,进一步了解情况,在抽取的5户中再随机抽取3户,求这3户中恰好有2户生二孩的概率.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
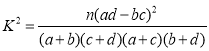 (其中
(其中![]() ).
).
【题目】某汽车公司生产新能源汽车,2019年3-9月份销售量(单位:万辆)数据如下表所示:
月份 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
销售量 (万辆) | 3.008 | 2.401 | 2.189 | 2.656 | 1.665 | 1.672 | 1.368 |
(1)某企业响应国家号召,购买了6辆该公司生产的新能源汽车,其中四月份生产的4辆,五月份生产的2辆,6辆汽车随机地分配给A,B两个部门使用,其中A部门用车4辆,B部门用车2辆.现了解该汽车公司今年四月份生产的所有新能源汽车均存在安全隐患,需要召回.求该企业B部门2辆车中至多有1辆车被召回的概率;
(2)经分析可知,上述数据近似分布在一条直线附近.设![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,根据表中数据可计算出
,根据表中数据可计算出![]() ,试求出
,试求出![]() 的值,并估计该厂10月份的销售量.
的值,并估计该厂10月份的销售量.