题目内容
【题目】一只红玲虫的产卵数
和温度
有关.现收集了7组观测数据如下表:
温度 | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
产卵数 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
为了预报一只红玲虫在
时的产卵数，根据表中的数据建立了与的两个回归模型.模型①:先建立与的指数回归方程
，然后通过对数变换
，把指数关系变为
与；模型②:先建立与的二次回归方程
，然后通过变换
，把二次关系变为与
的线性回归方程:
.
（1）分别利用这两个模型，求一只红玲虫在时产卵数的预测值；
（2）你认为用哪个模型得到的预测值更可靠?并说明理由.（参考数据:模型①的残差平方和
，模型①的相关指数
；模型②的残差平方和
，模型②的相关指数
；
，
，
；
，
，
，
，
，
，
）
【答案】（1）
，
（2）模型①得到的预测值更可靠，理由见解析
【解析】
（1）把
分别代入两个模型求解即可；
（2）通过残差及相关指数的大小进行判定比较.
(1)当时，根据模型①，得
， 
，根据模型②，得
.
（2）模型①得到的预测值更可靠.理由1:因为模型①的残差平方和
小于模型②的残差平方和
，所以模型①得到的预测值比模型②得到的预测值更可靠；理由2:模型①的相关指数
大于模型②的相关指数
，所以模型①得到的预测值比模型②得到的预测值更可靠；理由3:因为由模型①，根据变换后的线性回归方程
计算得到的样本点分布在一条直线的附近；而由模型②，根据变换后的线性回归方程
得到的样本点不分布在一条直线的周围，因此模型②不适宜用来拟合
与
的关系；所以模型①得到的预测值比模型②得到的预测值更可靠.（注:以上给出了3种理由，考生答出其中任意一种或其他合理理由均可得）
【题目】某花圃为提高某品种花苗质量，开展技术创新活动，在
实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况，分别在实验地随机抽取各50株，对每株进行综合评分，将每株所得的综合评分制成如图所示的频率分布直方图，记综合评分为80及以上的花苗为优质花苗.
（1）求图中
的值，并估计该品种花苗综合评分的平均数（同一组中的数据用该组区间的中点值为代表）；
（2）填写下面的列联表，并判断是否有99%的把握认为优质花苗与培驻外方法有关.
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合计 |
附：下面的临界值表仅供参考.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
（参考公式：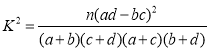
，其中
）
