题目内容
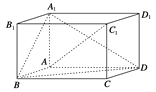
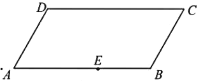
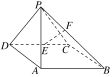
【题目】如图,在四棱锥PABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,AB=DP=![]() ,E为CD的中点,点F在线段PB上.试确定点F的位置,使得直线EF与平面PDC所成的角和直线EF与平面ABCD所成的角相等.
,E为CD的中点,点F在线段PB上.试确定点F的位置,使得直线EF与平面PDC所成的角和直线EF与平面ABCD所成的角相等.
【答案】当![]() 时,直线EF与平面PDC所成的角和直线EF与平面ABCD所成的角相等
时,直线EF与平面PDC所成的角和直线EF与平面ABCD所成的角相等
【解析】
由已知可证PA⊥底面ABCD,由余弦定理求出![]() ,进而有
,进而有![]() ,以A为坐标原点,以DA,AC,AP所在直线为x轴,y轴,z轴,建立空间直角坐标系Axyz,求出
,以A为坐标原点,以DA,AC,AP所在直线为x轴,y轴,z轴,建立空间直角坐标系Axyz,求出![]() 坐标,设
坐标,设![]() =λ(λ∈[0,1]),求出平面PDC的法向量坐标,而平面ABCD的一个法向量为
=λ(λ∈[0,1]),求出平面PDC的法向量坐标,而平面ABCD的一个法向量为![]() =(0,0,1),按照空间向量的线面角公式,即可求解.
=(0,0,1),按照空间向量的线面角公式,即可求解.
∵侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,
PA⊥AD,PA平面PAD,∴PA⊥底面ABCD. 以A为坐标原点,
在![]() 中,
中,![]() ,
,
![]()
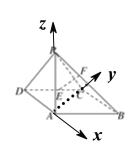
以DA,AC,AP所在直线为x轴,y轴,z轴,
建立如图所示的空间直角坐标系Axyz,
则A(0,0,0),D(-2,0,0),C(0,2,0),
B(2,2,0),E(-1,1,0),P(0,0,2),
∴![]() =(0,2,-2),
=(0,2,-2),![]() =(-2,0,-2),
=(-2,0,-2),
![]() =(2,2,-2).设
=(2,2,-2).设![]() =λ(λ∈[0,1]),
=λ(λ∈[0,1]),
则![]() =(2λ,2λ,-2λ),F(2λ,2λ,-2λ+2),
=(2λ,2λ,-2λ),F(2λ,2λ,-2λ+2),
∴![]() =(2λ+1,2λ-1,-2λ+2),
=(2λ+1,2λ-1,-2λ+2),
平面ABCD的一个法向量为![]() =(0,0,1).
=(0,0,1).
设平面PDC的法向量为![]() =(x,y,z),
=(x,y,z),
则∴![]() ,令x=1,得
,令x=1,得![]() =(1,-1,-1).
=(1,-1,-1).
∵直线EF与平面PDC所成的角和此直线与平面ABCD所成的角相等,
![]()
![]() ,
,
即![]() ,∴2-2λ=
,∴2-2λ=![]() ,解得
,解得![]() ,
,
∴当![]() 时,直线EF与平面PDC所成的角和直线EF与平面ABCD所成的角相等.
时,直线EF与平面PDC所成的角和直线EF与平面ABCD所成的角相等.

【题目】足球是世界普及率最高的运动,我国大力发展校园足球.为了解本地区足球特色学校的发展状况,社会调查小组得到如下统计数据:
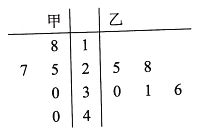
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校y(百个) | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱.
(已知:![]() ,则认为y与x线性相关性很强;
,则认为y与x线性相关性很强;![]() ,则认为y与x线性相关性一般;
,则认为y与x线性相关性一般;![]() ,则认为y与x线性相关性较):
,则认为y与x线性相关性较):
(2)求y关于x的线性回归方程,并预测A地区2020年足球特色学校的个数(精确到个).
参考公式和数据: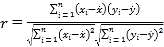 ,
,
![]()
![]()
![]() ,
,
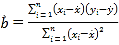
![]() .
.