题目内容
设各项为正数的数列 的前
的前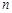 和为
和为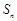 ,且
,且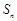 满足:
满足: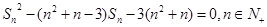 .等比数列
.等比数列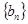 满足:
满足: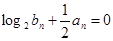 .
.
(Ⅰ)求数列 ,
,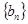 的通项公式;
的通项公式;
(Ⅱ)设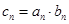 ,求数列
,求数列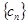 的前
的前 项的和
项的和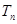 ;
;
(Ⅲ)证明:对一切正整数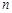 ,有
,有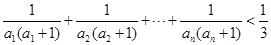 .
.
(1)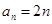 ,
, ;(2)
;(2)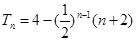 ;(3)证明略.
;(3)证明略.
解析试题分析:(1)给出 与
与 的关系,求
的关系,求 ,常用思路:一是利用
,常用思路:一是利用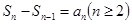 转化为
转化为 的递推关系,再求其通项公式;二是转化为
的递推关系,再求其通项公式;二是转化为 的递推关系,先求出
的递推关系,先求出 与
与 的关系,再求
的关系,再求 ;由
;由 推
推 时,别漏掉
时,别漏掉 这种情况,大部分学生好遗忘;(2)一般地,如果数列
这种情况,大部分学生好遗忘;(2)一般地,如果数列 是等差数列,
是等差数列,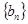 是等比数列,求数列
是等比数列,求数列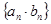 的前
的前 项的和1时,可采用错位相减法求和,一般是和式两边同乘以等比数列
项的和1时,可采用错位相减法求和,一般是和式两边同乘以等比数列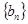 的公比,然后做差求解;(3)利用不等式放缩时掌握好规律,怎样从条件证明出结论.
的公比,然后做差求解;(3)利用不等式放缩时掌握好规律,怎样从条件证明出结论.
试题解析:当 时,
时, 即
即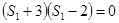 ,又
,又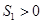 ,
,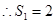 ,即
,即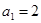
当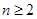 时,
时,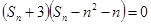 ,又
,又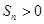 ,
,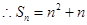
当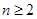 时,
时,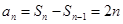
又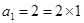
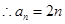
由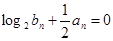 ,得
,得

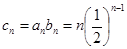
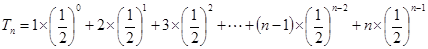
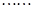 (1)
(1)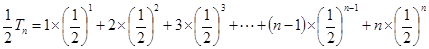
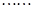 (2)
(2) 得
得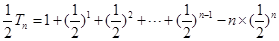
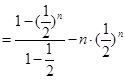
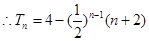 .............................................9分
.............................................9分
(Ⅲ)当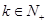 时
时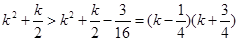
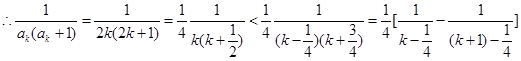
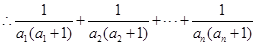
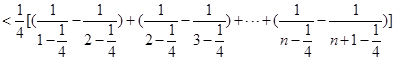
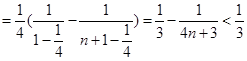 .....................14分
.....................14分
考点:(1)求数列的通项公式;(2)错位相减求数列的和;(3)证明恒成立的问题.

练习册系列答案
相关题目
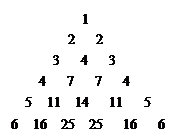
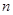 行首尾两数均为
行首尾两数均为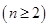 第
第 个数是
个数是  的通项公式
的通项公式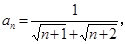 其前
其前 项和
项和 ,则
,则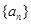 的前
的前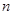 项和为
项和为 ,且
,且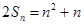 2.
2.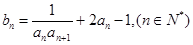 求数列
求数列 的前
的前 项和
项和 ,数列
,数列 满足
满足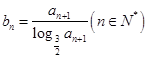 .
.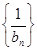 的前
的前 .
.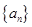 满足:
满足: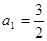 ,
, 
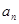 ;
; 满足
满足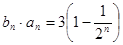 ,求数列
,求数列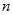 项和.
项和. 的前
的前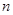 项和为
项和为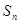 ,且2
,且2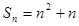 .
.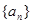 的通项公式;
的通项公式;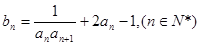 求数列
求数列 的前
的前 的前
的前 项和
项和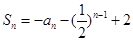 (
( ,求证数列
,求证数列 是等差数列,并求数列
是等差数列,并求数列 ,
, ,试比较
,试比较 与
与 的大小,并予以证明
的大小,并予以证明 中,
中,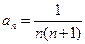 ,前n项和为Sn,则S2009=______________。
,前n项和为Sn,则S2009=______________。