题目内容
如图,它满足: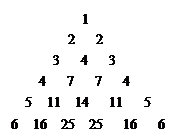
(1)第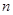 行首尾两数均为
行首尾两数均为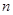 ;
;
(2)表中的递推关系类似杨辉三角,则第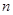 行
行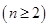 第
第 个数是
个数是
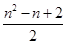
解析试题分析:根据图上规律,第n行第2个数等于第(n-1)个三角数 + 1
三角数就是形如T(n) = 1+2+3……+n的数。
也就是说,
第2行第2个数 =" T(1)" + 1 =" 1" + 1 = 2
第3行第2个数 =" T(2)" + 1 =" 1+2" + 1 = 4
第4行第2个数 =" T(3)" + 1 =" 1+2+3" + 1 = 7
第5行第2个数 =" T(4)" + 1 =" 1+2+3+4" + 1 = 11
第6行第2个数 =" T(5)" + 1 =" 1+2+3+4+5" + 1 = 16
因此,第n行(n≥2)第2个数是T(n-1) + 1 = 1+2+3+……+(n-1) + 1 = 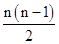 + 1=
+ 1=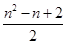 .
.
考点:本题主要考查归纳推理,等差数列的求和。
点评:简单题,归纳推理,就是从个别性知识推出一般性结论的推理。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
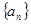 中,
中, ,
, 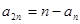 ,
,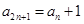 ,则
,则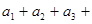
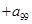 = .
= . 的通项公式
的通项公式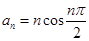 ,其前
,其前 项和为
项和为 ,则
,则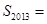 .
.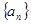 中,各项均为正数,且
中,各项均为正数,且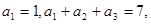 则数列
则数列 ;前n项和
;前n项和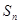 = .
= . 的前
的前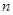 项和为
项和为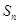 ,
, ,
,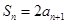 ,,则
,,则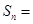 .
.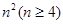 个正数排成
个正数排成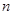 行
行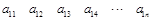
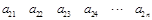
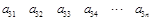
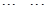
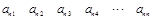
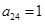 ,
,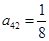 ,
,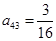 ,则
,则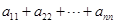 = 。
= 。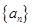 的前n项和为
的前n项和为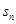 ,已知数列
,已知数列 是首项和公比都为3的等比数列,则数列
是首项和公比都为3的等比数列,则数列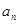 =_____________________
=_____________________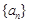 中,
中,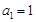 ,
,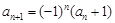 ,记
,记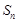 为
为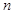 项的和,则
项的和,则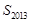 = ;
= ; 的前
的前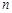 和为
和为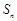 ,且
,且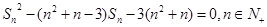 .等比数列
.等比数列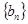 满足:
满足: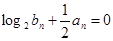 .
.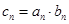 ,求数列
,求数列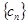 的前
的前 项的和
项的和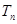 ;
;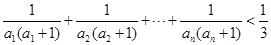 .
.