Question

【题目】在直角坐标系中，已知椭圆的上下两个焦点分别为，且，椭圆过点．

(1)求椭圆的标准方程；

(2)设椭圆的一个顶点为，直线交椭圆于另一个点，求的面积．

Answer 1

【答案】（1）（2）

【解析】

（1）法1：由题意可得，焦点，，从而，求出a，b，由此能求出椭圆的标准方程．

法2：由题意可得，焦点，，椭圆过点），列方程组求出a，b，由此能求出椭圆的方程．

法3：由题意可得，焦点，，椭圆过点，得，求出a，b，由此能求出椭圆的方程．

（2）直线BF2的斜率，从而直线BF2的方程为，联立，得点N的横坐标为，由此能求出△F1BN的面积．

（1）〖解法1〗由题意可得，焦点，

，得，

，

所以椭圆的标准方程是

〖解法2〗由题意可得，焦点，

又椭圆过点，∴

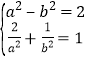
解得，

∴椭圆的方程为．

〖解法3〗由题意可得，焦点，

又椭圆过点，∴

∴，∵ ∴可解得，

∴椭圆的方程为．

（2） ，直线的斜率

直线的方程为，即

联立，得点的横坐标为

又

∴

综上，的面积为.