题目内容
(本小题满分14分)数列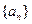 和数列
和数列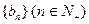 由下列条件确定:
由下列条件确定:
①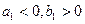 ;
;
②当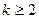 时,
时,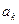 与
与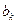 满足如下条件:当
满足如下条件:当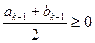 时,
时,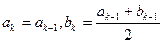 ;当
;当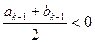 时,
时,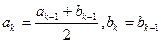 。
。
解答下列问题:
(Ⅰ)证明数列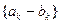 是等比数列;
是等比数列;
(Ⅱ)求数列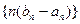 的前n项和为
的前n项和为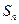 ;
;
(Ⅲ)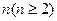 是满足
是满足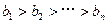 的最大整数时,用
的最大整数时,用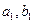 表示n的满足的条件。
表示n的满足的条件。
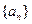 和数列
和数列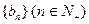 由下列条件确定:
由下列条件确定:①
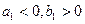 ;
;②当
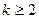 时,
时,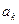 与
与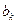 满足如下条件:当
满足如下条件:当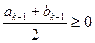 时,
时,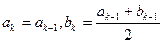 ;当
;当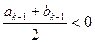 时,
时,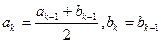 。
。解答下列问题:
(Ⅰ)证明数列
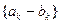 是等比数列;
是等比数列;(Ⅱ)求数列
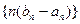 的前n项和为
的前n项和为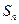 ;
;(Ⅲ)
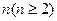 是满足
是满足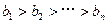 的最大整数时,用
的最大整数时,用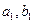 表示n的满足的条件。
表示n的满足的条件。(Ⅰ)当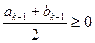 时,
时,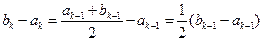
当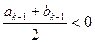 时,
时,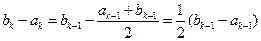
所以不论哪种情况,都有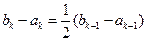 ,又显然
,又显然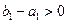 ,
,
故数列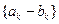 是等比数列
是等比数列
(Ⅱ)由(Ⅰ)知,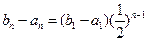 ,故
,故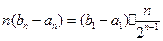
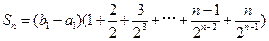
所以,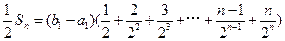
所以,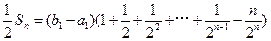 ,
,
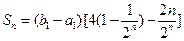
(Ⅲ)当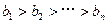
 时,
时,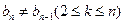
由②知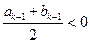 不成立,故
不成立,故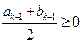 从而对于
从而对于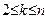 ,有
,有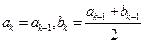 ,于是
,于是 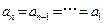 ,故
,故
若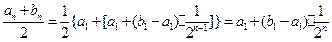 ,
,
若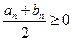 ,则
,则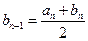
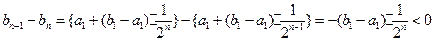
所以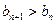 ,这与n是满足
,这与n是满足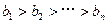
 的最大整数矛盾。
的最大整数矛盾。
因此n是满足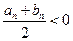 的最小整数,
的最小整数,
而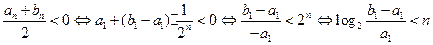
因而,n是满足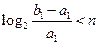 最小整数。
最小整数。
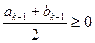 时,
时,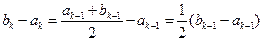
当
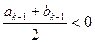 时,
时,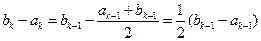
所以不论哪种情况,都有
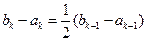 ,又显然
,又显然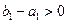 ,
,故数列
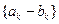 是等比数列
是等比数列(Ⅱ)由(Ⅰ)知,
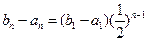 ,故
,故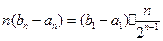
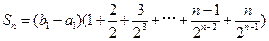
所以,
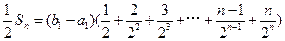
所以,
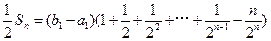 ,
,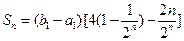
(Ⅲ)当
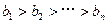
 时,
时,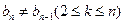
由②知
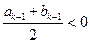 不成立,故
不成立,故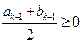 从而对于
从而对于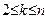 ,有
,有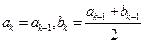 ,于是
,于是 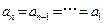 ,故
,故
若
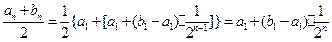 ,
,若
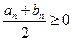 ,则
,则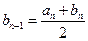
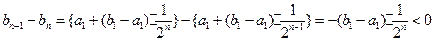
所以
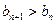 ,这与n是满足
,这与n是满足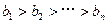
 的最大整数矛盾。
的最大整数矛盾。因此n是满足
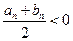 的最小整数,
的最小整数,而
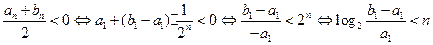
因而,n是满足
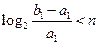 最小整数。
最小整数。同答案

练习册系列答案
相关题目
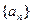 的前
的前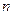 项和为
项和为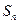 ,且满足
,且满足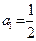 ,
,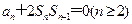 .(1)问:数列
.(1)问:数列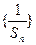 是否为等差数列?并证明你的结论;(2)求
是否为等差数列?并证明你的结论;(2)求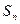 和
和 ;(3)求证:
;(3)求证: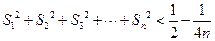 .
.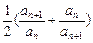 (n∈N*),求
(n∈N*),求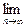 (b1+b2+b3+…+bn-n).
(b1+b2+b3+…+bn-n).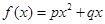 ,其中p>0,p+q>1。对于数列
,其中p>0,p+q>1。对于数列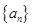 ,设它的前n项之和为
,设它的前n项之和为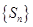 ,且
,且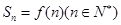 。
。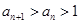 (3)证明:点
(3)证明:点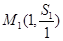 ,
,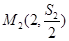 ,
,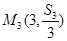 ,
, ,
,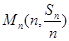 共线
共线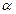 为锐角,且
为锐角,且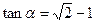 ,
,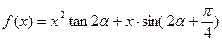 ,数列{an}的首项
,数列{an}的首项 .
.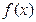 的表达式;
的表达式;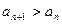 ;
; 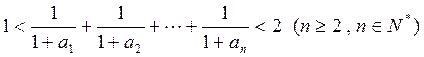
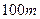 ,降低
,降低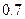 ℃,已知山顶处的温度是
℃,已知山顶处的温度是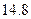 ℃,山脚处的温度为
℃,山脚处的温度为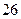 ℃,问此山相对于山脚处的高度是多少米.
℃,问此山相对于山脚处的高度是多少米. 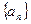 中,
中,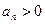 ,其公差
,其公差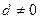 ;数列
;数列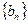 是等比数列,
是等比数列,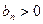 ,其公比
,其公比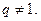
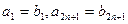 ,试比较
,试比较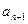 与
与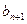 的大小,说明理由;
的大小,说明理由;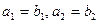 ,试比较
,试比较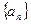 中,
中,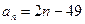 ,当数列
,当数列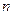 项和
项和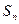 取得最小值时,
取得最小值时,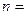 .
.