题目内容
((本小题满分12分)
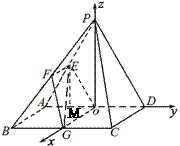
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PA、PB、BC的中点.
(1)求证:EF 平面PAD;
平面PAD;
(2)求平面EFG与平面ABCD所成锐二面角的大小;
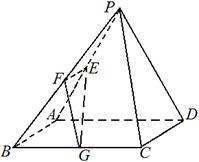
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PA、PB、BC的中点.
(1)求证:EF
 平面PAD;
平面PAD;(2)求平面EFG与平面ABCD所成锐二面角的大小;

解:方法1:( I)证明:∵平面PAD⊥平面ABCD,
I)证明:∵平面PAD⊥平面ABCD, ,
,

∴ 平面PAD, )
平面PAD, )
∵E、F为PA、PB的中点,
∴EF//AB,∴EF 平面PAD; …………4分
平面PAD; …………4分
(II)解:过P作AD的垂线,垂足为O,
 ∵
∵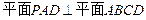 ,则PO
,则PO  平面ABCD.
平面ABCD.
取AO中点M,连OG,,EO,EM,
∵EF //AB//OG,
∴OG即为面EFG与面ABCD的交线
又EM//OP,则EM 平面ABCD.且OG
平面ABCD.且OG AO,
AO,
故OG EO ∴
EO ∴ 即为所求 …………8分
即为所求 …………8分
 ,EM=
,EM= OM=1
OM=1
∴tan =
= 故
故  =
=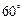
∴平面EFG与平面ABCD所成 锐二面角的大小是
锐二面角的大小是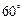 …………12分
…………12分
方法2:(I)证明:过P作P O AD于O,∵
AD于O,∵ ,
,
则PO 平面ABCD,连OG,以OG,OD,OP为x、y、z轴建立空间坐标系, …………2分
平面ABCD,连OG,以OG,OD,OP为x、y、z轴建立空间坐标系, …………2分
∵PA=PD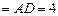 ,∴
,∴ ,
,
得 ,
,
 , …………(4分)
, …………(4分)
故 ,
,
∵ ,
,
∴EF 平面PAD; …………4分
平面PAD; …………4分
(II)解: ,
,
设平面EFG的一个法向量为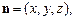
则 ,
,  , …………8分
, …………8分
平面ABCD的一个法向量为 ……(12分)
……(12分)
平面EFG与平面ABCD所成锐二面角的余弦值是:
 ,锐二面角的大小是
,锐二面角的大小是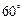 ; …………12分
; …………12分
 I)证明:∵平面PAD⊥平面ABCD,
I)证明:∵平面PAD⊥平面ABCD, ,
,
∴
 平面PAD, )
平面PAD, )∵E、F为PA、PB的中点,
∴EF//AB,∴EF
 平面PAD; …………4分
平面PAD; …………4分(II)解:过P作AD的垂线,垂足为O,
 ∵
∵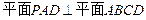 ,则PO
,则PO  平面ABCD.
平面ABCD. 取AO中点M,连OG,,EO,EM,
∵EF //AB//OG,
∴OG即为面EFG与面ABCD的交线
又EM//OP,则EM
 平面ABCD.且OG
平面ABCD.且OG AO,
AO,故OG
 EO ∴
EO ∴ 即为所求 …………8分
即为所求 …………8分 ,EM=
,EM= OM=1
OM=1 ∴tan
 =
= 故
故  =
=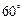
∴平面EFG与平面ABCD所成
 锐二面角的大小是
锐二面角的大小是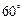 …………12分
…………12分方法2:(I)证明:过P作P O
 AD于O,∵
AD于O,∵ ,
, 则PO
 平面ABCD,连OG,以OG,OD,OP为x、y、z轴建立空间坐标系, …………2分
平面ABCD,连OG,以OG,OD,OP为x、y、z轴建立空间坐标系, …………2分∵PA=PD
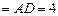 ,∴
,∴ ,
,得
 ,
, , …………(4分)
, …………(4分)故
 ,
,∵
 ,
,∴EF
 平面PAD; …………4分
平面PAD; …………4分(II)解:
 ,
,设平面EFG的一个法向量为
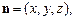
则
 ,
,  , …………8分
, …………8分平面ABCD的一个法向量为
 ……(12分)
……(12分)平面EFG与平面ABCD所成锐二面角的余弦值是:
 ,锐二面角的大小是
,锐二面角的大小是 ; …………12分
; …………12分略

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
 F 在 EA 上且 B1F⊥AE,试求点 F 的坐标;
F 在 EA 上且 B1F⊥AE,试求点 F 的坐标;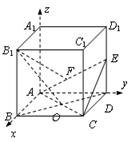
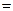 a,AD
a,AD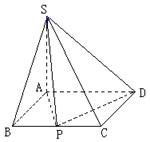
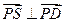 .
. 个单位法向量
个单位法向量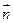
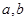 分别在平面
分别在平面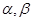 内,且平面
内,且平面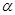 与
与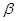 的交线为
的交线为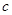 ,则直线
,则直线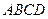 中,
中,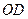 垂直平分
垂直平分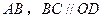 ,且
,且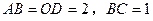 ,现将四边形
,现将四边形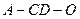 的正弦值;
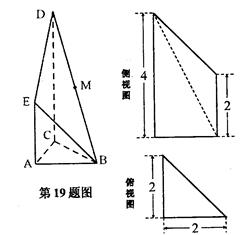
的正弦值; 的体积.
的体积.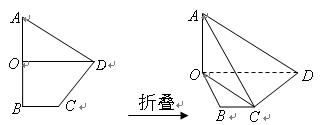
 ?若存在,确定点N的位置;
?若存在,确定点N的位置; 若不存在,请说明理由.
若不存在,请说明理由. 
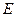 为正方体
为正方体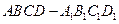 的棱
的棱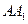 的中点,
的中点,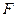 为棱
为棱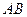 上一点,
上一点,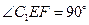 ,则
,则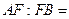 ( )
( )