题目内容
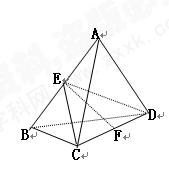
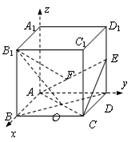
(满分12分)正方体ABCD-A1B1C1D1 的棱长为 2,且AC 与BD 交于点O,E 为棱DD1 中点,以A 为原点,建立空间直角坐标系A-xyz,如图所示.
(Ⅰ)求证:B1O⊥平面EAC;
(Ⅱ)若点 F 在 EA 上且 B1F⊥AE,试求点 F 的坐标;
F 在 EA 上且 B1F⊥AE,试求点 F 的坐标;
(Ⅲ)求二面角B1-EA-C 的正弦值.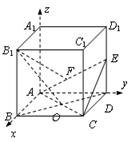
(Ⅰ)求证:B1O⊥平面EAC;
(Ⅱ)若点
 F 在 EA 上且 B1F⊥AE,试求点 F 的坐标;
F 在 EA 上且 B1F⊥AE,试求点 F 的坐标;(Ⅲ)求二面角B1-EA-C 的正弦值.

(Ⅰ)见解析
(Ⅱ) F (0, , )
(Ⅲ)二面角B1-EA-C的正弦值为
(Ⅱ) F (0, , )
(Ⅲ)二面角B1-EA-C的正弦值为
证明:(I) 由题设知下列各点的坐标A(0, 0, 0), B(2, 0, 0), C (2, 2, 0),
D (0, 2, 0), E (0, 2, 1), B1(2, 0, 2).
∵O是正方形ABCD的中心,∴O (1, 1, 0).
∴= (-1, 1, -2),=" (2," 2, 0),=" (0," 2, 1).2分
 ∴·= (-1, 1, -2)·(2, 2, 0)
∴·= (-1, 1, -2)·(2, 2, 0)
= -1·2 + 1·2-2·0 = 0.
·= (-1, 1, -2)·(0, 2, 1)
= -1·0 + 1 ·2-2·1 = 0.
·2-2·1 = 0.
∴⊥,⊥,
即B1O ⊥AC,B1O⊥AE,
∴B1O⊥平面ACE. 4分
(II) 由F点在AE上,可设点F的坐标为F (0, 2l, l), 5分
则= (-2, 2l, l-2). 6分
∵⊥,
∴·= (-2, 2l, l-2)·(0, 2, 1) = 5l-2 = 0, 7分
∴ l = ,
∴F (0, , ). 8分
(III) ∵B1O⊥平面EAC,B1F⊥AE,连结OF,由三垂线定理的逆定理得OF⊥AE.
∴∠OFB1即为二面角B1-EA-C的平面角. 9分
∴ | | = = . 10分
| = = . 10分
又= (-2, ,-),
∴ | | = = . 11分
在Rt△B1OF中,sin∠B1FO = = .
故二面角B1-EA-C的正弦值为. 12分
D (0, 2, 0), E (0, 2, 1), B1(2, 0, 2).
∵O是正方形ABCD的中心,∴O (1, 1, 0).
∴= (-1, 1, -2),=" (2," 2, 0),=" (0," 2, 1).2分
 ∴·= (-1, 1, -2)·(2, 2, 0)
∴·= (-1, 1, -2)·(2, 2, 0)= -1·2 + 1·2-2·0 = 0.
·= (-1, 1, -2)·(0, 2, 1)
= -1·0 + 1
 ·2-2·1 = 0.
·2-2·1 = 0. ∴⊥,⊥,
即B1O ⊥AC,B1O⊥AE,
∴B1O⊥平面ACE. 4分
(II) 由F点在AE上,可设点F的坐标为F (0, 2l, l), 5分
则= (-2, 2l, l-2). 6分
∵⊥,
∴·= (-2, 2l, l-2)·(0, 2, 1) = 5l-2 = 0, 7分
∴ l = ,
∴F (0, , ). 8分
(III) ∵B1O⊥平面EAC,B1F⊥AE,连结OF,由三垂线定理的逆定理得OF⊥AE.
∴∠OFB1即为二面角B1-EA-C的平面角. 9分
∴ |
 | = = . 10分
| = = . 10分又= (-2, ,-),
∴ | | = = . 11分
在Rt△B1OF中,sin∠B1FO = = .
故二面角B1-EA-C的正弦值为. 12分

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 平面PAD;
平面PAD;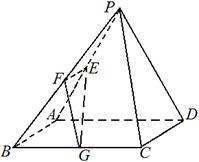
 中,
中,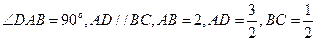
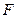 以
以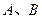 为焦点且过点
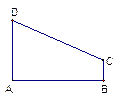
为焦点且过点 ,
,
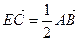 是否存在斜率
是否存在斜率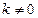 的直线
的直线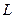 与椭圆
与椭圆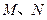 两点,且
两点,且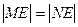 ,若存在,求
,若存在,求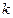 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。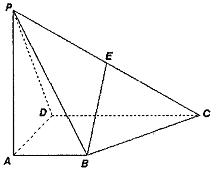
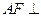 平面PCD;(2)求证:平面PCE⊥平面PCD.
平面PCD;(2)求证:平面PCE⊥平面PCD.
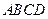 中,
中,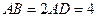 ,
,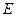 为
为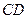 的中点,沿
的中点,沿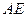 将
将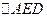 折起,使
折起,使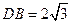 ,
,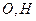 分别为
分别为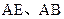 的中点。
的中点。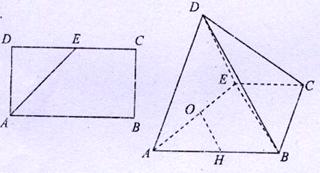
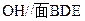
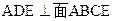
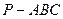 中,
中,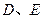 分别是
分别是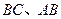 的中点,
的中点,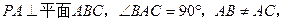
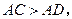
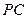 与
与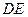 所成的角为
所成的角为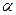 ,
,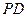 与平面
与平面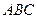 所成的角为
所成的角为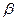 ,二面角
,二面角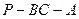 的平面角为
的平面角为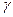 ,则
,则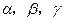 的大小关系是 ( )
的大小关系是 ( ) 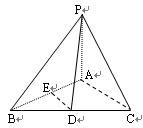
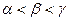
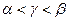
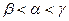
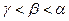
 是边长为
是边长为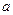 的正三角形
的正三角形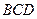 所在平面外一点,
所在平面外一点,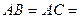
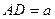 ,
,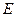 、
、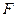 分别是
分别是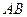 、
、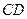 中点,
中点,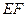 为异面直线
为异面直线