题目内容
已知异面直线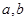 分别在平面
分别在平面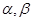 内,且平面
内,且平面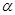 与
与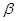 的交线为
的交线为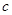 ,则直线
,则直线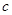 与
与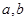 的位置关系是
的位置关系是
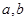 分别在平面
分别在平面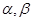 内,且平面
内,且平面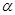 与
与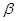 的交线为
的交线为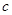 ,则直线
,则直线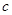 与
与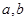 的位置关系是
的位置关系是A.与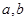 都平行 都平行 | B.至多与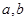 中的一条相交 中的一条相交 |
C.与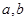 都不平行 都不平行 | D.至少与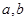 中的一条相交 中的一条相交 |
D
专题:探究型.
分析:由平行公理,我们可以判断A,D的正误,根据异面直线判定定理,可以判断B的正误,根据异面直线夹角的定义中平移直线法,可以判断C的正误,进而得到答案.
解答:解:若直线c与a,b均平行,由平行公理,可得a∥b,这与a,b异面矛盾,故A错误;
当a,b与c相交,但交点不同为一点时,a,b异面,故B错误;
如果a,b与c一条平行,一条相交,a,b异面,故C错误;
但如果c与a,b均不相交,则直线c与a,b均平行,由A中结论,可得假设不成立,故D正确;
故选D
点评:本题考查的知识点是空间中直线与直线之间的位置关系,其中熟练掌握空间直线不同位置关系的定义及几何特征是解答本题的关键.

练习册系列答案
相关题目
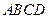 的一组对棱
的一组对棱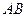 、
、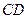 的平面截此四面体(如图).
的平面截此四面体(如图).
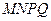 是平行四边形;
是平行四边形;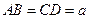 .求证:四边形
.求证:四边形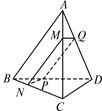
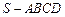 中,
中,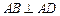 ,
,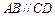 ,
,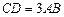 ,平面
,平面 平面
平面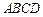 ,
,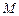 是线段
是线段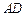 上一点,
上一点,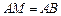 ,
,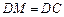 ,
,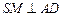 .
.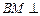 平面
平面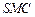 ;
;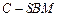 与四棱锥
与四棱锥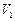 与
与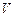 ,求
,求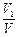 的值.
的值.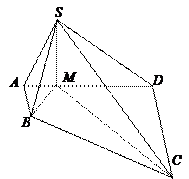
 平面PAD;
平面PAD;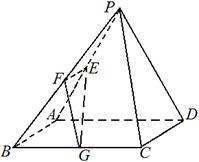
 相交的线段
相交的线段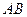 ,其长度为10cm,两端点
,其长度为10cm,两端点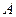 、
、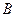 到平面
到平面 面a所成的角是 .
面a所成的角是 . 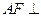 平面PCD;(2)求证:平面PCE⊥平面PCD.
平面PCD;(2)求证:平面PCE⊥平面PCD.
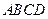 中,
中,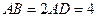 ,
,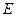 为
为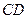 的中点,沿
的中点,沿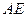 将
将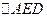 折起,使
折起,使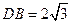 ,
,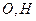 分别为
分别为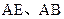 的中点。
的中点。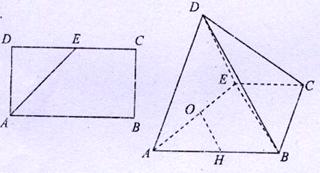
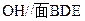
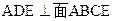
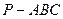 中,
中,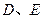 分别是
分别是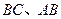 的中点,
的中点,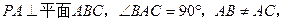
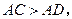
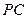 与
与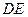 所成的角为
所成的角为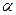 ,
,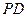 与平面
与平面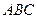 所成的角为
所成的角为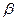 ,二面角
,二面角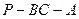 的平面角为
的平面角为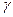 ,则
,则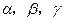 的大小关系是 ( )
的大小关系是 ( ) 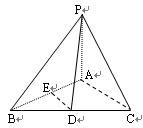
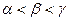
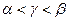
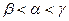
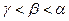
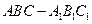 中,已知
中,已知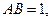 点
点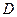 在棱
在棱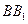 上,且
上,且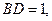 且
且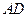
 与平面
与平面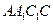 所成的角的正弦值是_
所成的角的正弦值是_ ___________.
___________.