题目内容
(本小题满分12分)
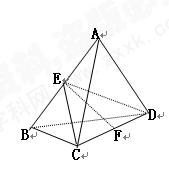
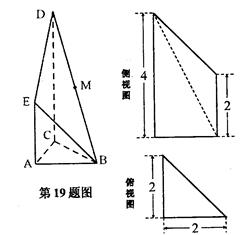
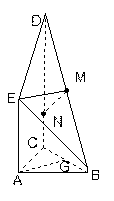
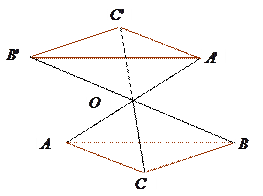
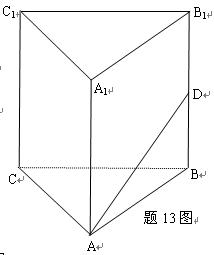
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(I)求出该几何体的体积;
(II)求证:EM∥平面ABC;
(III)试问在棱DC上是否存在点N,使NM⊥平面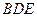 ?若存在,确定点N的位置;
?若存在,确定点N的位置; 若不存在,请说明理由.
若不存在,请说明理由.
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(I)求出该几何体的体积;
(II)求证:EM∥平面ABC;
|
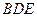 ?若存在,确定点N的位置;
?若存在,确定点N的位置; 若不存在,请说明理由.
若不存在,请说明理由. 略
解法一:由题意,Ea⊥平面ABC,DC⊥平面ABC,AE//DC,AE=2,
DC=4,AB⊥AC,且AE=AC=2,
(I)∵EA⊥平面ABC,∴ea⊥ab, 又ab⊥ac,
 ∴ab⊥平面acde , …………2分
∴ab⊥平面acde , …………2分
∴四棱锥b-acde的高h=ab=2,梯形acde的面积S= 6
∴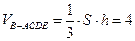 ,
,
即所求几何体的体积为4 ………………4分 (II)证明:∵m为db的中点,取bc中点G,连接em,mG,aG,
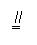 ∴ mG∥DC,且
∴ mG∥DC,且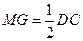
∴ mG ae,∴四边形aGme为平行四边形,……6分
∴em∥aG,又AG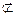 平面ABC
平面ABC
AG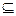 平面ABC,
平面ABC,
∴EM∥平面ABC.……8分
(III)由(II)知,em∥aG,
又∵平面BCD⊥底面ABC,aG⊥bc,∴AG⊥平面BCD
∴EM⊥平面BCD,又∵EM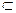 平面BDE,
平面BDE,
∴平面BDE⊥平面BCD 10分
在平面BCD中,过M作MN⊥DB交DC于点N,
∴MN⊥平面BDE 点n即为所求的点 ………………10分
∵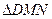 ∽
∽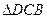
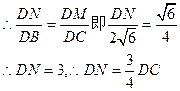
∴边DC上存在点N,满足DN=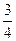 DC时,有MN⊥平面BDE. …………12分
DC时,有MN⊥平面BDE. …………12分
解法二:(I)(同解法一) …………4分
(II)由(I)知EA⊥AB,EA⊥AC,AB⊥AC。
∴以A为原点如图建立空间直角坐标系A—xyz ………5分
则A(0,0,0),B(2,0,0),C(0,2,0),E(0,0,2),
D(0,2,4),M(1,1,2),
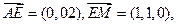 …………6分
…………6分
显然,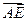 为平面ABC的法向量,
为平面ABC的法向量,
且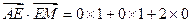 ="0 " …………7分
="0 " …………7分
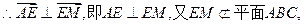
∴EM∥平面ABC. ……8分
(III)由(II)得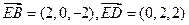 ,
,
设在棱DC上存在点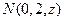 ,使MN⊥平面BDE,
,使MN⊥平面BDE,
则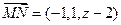 …………9分
…………9分
由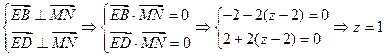 …………11分
…………11分
∴在棱DC上存在点N(0,2,1),使MN⊥平面BDE. …………12分
DC=4,AB⊥AC,且AE=AC=2,
(I)∵EA⊥平面ABC,∴ea⊥ab, 又ab⊥ac,
 ∴ab⊥平面acde , …………2分
∴ab⊥平面acde , …………2分∴四棱锥b-acde的高h=ab=2,梯形acde的面积S= 6
∴
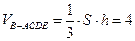 ,
,
|
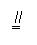 ∴ mG∥DC,且
∴ mG∥DC,且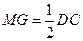
∴ mG ae,∴四边形aGme为平行四边形,……6分
∴em∥aG,又AG
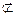 平面ABC
平面ABC AG
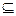 平面ABC,
平面ABC,∴EM∥平面ABC.……8分
(III)由(II)知,em∥aG,
又∵平面BCD⊥底面ABC,aG⊥bc,∴AG⊥平面BCD
∴EM⊥平面BCD,又∵EM
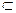 平面BDE,
平面BDE,∴平面BDE⊥平面BCD 10分
在平面BCD中,过M作MN⊥DB交DC于点N,
∴MN⊥平面BDE 点n即为所求的点 ………………10分
∵
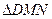 ∽
∽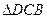
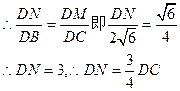
|
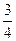 DC时,有MN⊥平面BDE. …………12分
DC时,有MN⊥平面BDE. …………12分解法二:(I)(同解法一) …………4分
(II)由(I)知EA⊥AB,EA⊥AC,AB⊥AC。
∴以A为原点如图建立空间直角坐标系A—xyz ………5分
则A(0,0,0),B(2,0,0),C(0,2,0),E(0,0,2),
D(0,2,4),M(1,1,2),
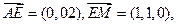 …………6分
…………6分显然,
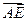 为平面ABC的法向量,
为平面ABC的法向量,且
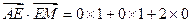 ="0 " …………7分
="0 " …………7分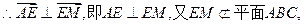
∴EM∥平面ABC. ……8分
(III)由(II)得
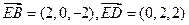 ,
,设在棱DC上存在点
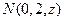 ,使MN⊥平面BDE,
,使MN⊥平面BDE,则
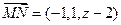 …………9分
…………9分由
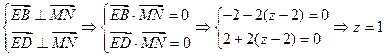 …………11分
…………11分∴在棱DC上存在点N(0,2,1),使MN⊥平面BDE. …………12分

练习册系列答案
相关题目
 ,
, ,
, 相交于
相交于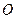 ,
,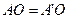 ,
,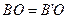 ,
, .
.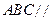 平面
平面 .
.
 平面PAD;
平面PAD;
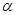 的斜线
的斜线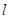 与平面
与平面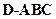 的外接球的球心O满足
的外接球的球心O满足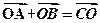 ,且外接球的体积为
,且外接球的体积为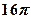 ,则该三棱锥的体积为 .
,则该三棱锥的体积为 . 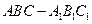 中,已知
中,已知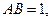 点
点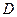 在棱
在棱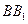 上,且
上,且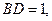 且
且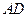
 与平面
与平面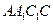 所成的角的正弦值是_
所成的角的正弦值是_ ___________.
___________.
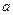 的正方体
的正方体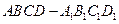 的8个顶点都在球
的8个顶点都在球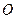 的表面上,E、F分别是棱
的表面上,E、F分别是棱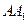 、
、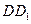 的中点,则直线EF被球
的中点,则直线EF被球 学
学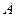 是边长为
是边长为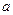 的正三角形
的正三角形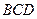 所在平面外一点,
所在平面外一点,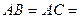
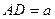 ,
,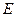 、
、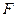 分别是
分别是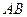 、
、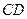 中点,
中点,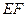 为异面直线
为异面直线