题目内容
已知三条直线l1:2x-y+a=0(a>0),直线l2:4x-2y-1=0和直线l3:x+y-1=0,且l1与l2的距离是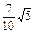 .
.
(1)求a的值;
(2)能否找到一点P,使得P点同时满足下列三个条件:
①P是第一象限的点;②P点到l1的距离是P点到l2的距离的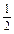 ;③P点到l1的距离与P点到l3的距离之比是
;③P点到l1的距离与P点到l3的距离之比是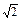 ∶
∶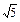 .若能,求P点坐标;若不能,说明理由.
.若能,求P点坐标;若不能,说明理由.
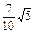 .
.(1)求a的值;
(2)能否找到一点P,使得P点同时满足下列三个条件:
①P是第一象限的点;②P点到l1的距离是P点到l2的距离的
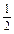 ;③P点到l1的距离与P点到l3的距离之比是
;③P点到l1的距离与P点到l3的距离之比是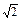 ∶
∶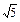 .若能,求P点坐标;若不能,说明理由.
.若能,求P点坐标;若不能,说明理由.(1)a=3(2)点P 即为同时满足三个条件的点
即为同时满足三个条件的点
 即为同时满足三个条件的点
即为同时满足三个条件的点(1)l2即为2x-y-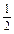 =0,
=0,
∴l1与l2的距离d=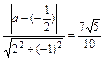 ,
,
∴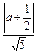 =
=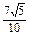 ,∴
,∴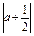 =
=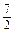 ,
,
∵a>0,∴a=3.
(2)假设存在这样的P点.
设点P(x0,y0),若P点满足条件②,则P点在与l1、l2平行的直线l′:2x-y+C=0上,
且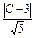 =
=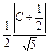 ,即C=
,即C=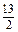 或C=
或C=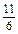 ,
,
∴2x0-y0+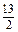 =0或2x0-y0+
=0或2x0-y0+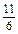 =0;
=0;
若P点满足条件③,由点到直线的距离公式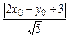 =
=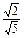 ×
×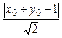 ,
,
即|2x0-y0+3|=|x0+y0-1|,
∴x0-2y0+4=0或3x0+2=0;
由于P点在第一象限,∴3x0+2=0不满足题意.
联立方程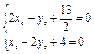 ,
,
解得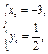 (舍去).
(舍去).
由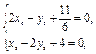 解得
解得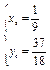
∴假设成立,点P 即为同时满足三个条件的点.
即为同时满足三个条件的点.
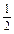 =0,
=0,∴l1与l2的距离d=
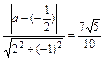 ,
,∴
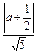 =
=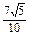 ,∴
,∴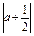 =
=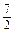 ,
,∵a>0,∴a=3.
(2)假设存在这样的P点.
设点P(x0,y0),若P点满足条件②,则P点在与l1、l2平行的直线l′:2x-y+C=0上,
且
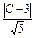 =
=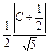 ,即C=
,即C=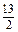 或C=
或C=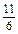 ,
,∴2x0-y0+
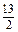 =0或2x0-y0+
=0或2x0-y0+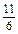 =0;
=0;若P点满足条件③,由点到直线的距离公式
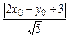 =
=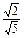 ×
×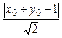 ,
,即|2x0-y0+3|=|x0+y0-1|,
∴x0-2y0+4=0或3x0+2=0;
由于P点在第一象限,∴3x0+2=0不满足题意.
联立方程
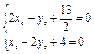 ,
,解得
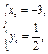 (舍去).
(舍去).由
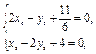 解得
解得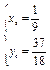
∴假设成立,点P
 即为同时满足三个条件的点.
即为同时满足三个条件的点.
练习册系列答案
相关题目
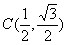 ,求△ABC的面积.
,求△ABC的面积. 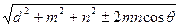 .
.
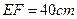
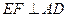


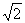
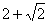
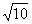
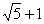
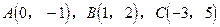
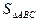 。
。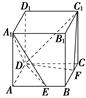

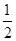
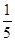

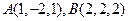 ,点
,点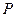 在
在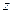 轴上,且
轴上,且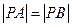 ,则点
,则点