题目内容
试在直线x-y+4=0上求一点P,使它到点M(-2,-4)、N(4,6)的距离相等.
解法一:由直线x-y+4=0,得y=x+4,点P在该直线上.
∴可设P点的坐标为(a,a+4).
由已知|PM|=|PN|,
∴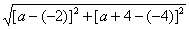
 ,
,
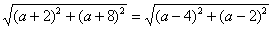 .
.
∴(a+2)2+(a+8)2=(a-4)2+(a-2)2.
解得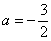 ,从而
,从而 .
.
∴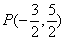 .
.
解法二:由于|PM|=|PN|,∴点P在线段MN的垂直平分线上.
由于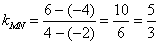 ,
,
∴线段MN的垂直平分线的斜率为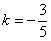 .
.
又MN的中点为(1,1),
∴线段MN的垂直平分线的方程为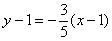 ,即
,即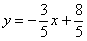 .
.
又∵点P在直线x-y+4=0上,
∴点P为直线x-y+4=0与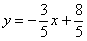 的交点?.
的交点?.
由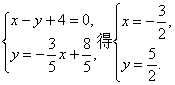
∴点P的坐标为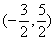 .
.
∴可设P点的坐标为(a,a+4).
由已知|PM|=|PN|,
∴
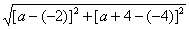
 ,
,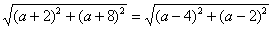 .
.∴(a+2)2+(a+8)2=(a-4)2+(a-2)2.
解得
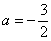 ,从而
,从而 .
.∴
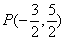 .
.解法二:由于|PM|=|PN|,∴点P在线段MN的垂直平分线上.
由于
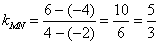 ,
,∴线段MN的垂直平分线的斜率为
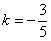 .
.又MN的中点为(1,1),
∴线段MN的垂直平分线的方程为
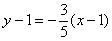 ,即
,即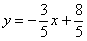 .
.又∵点P在直线x-y+4=0上,
∴点P为直线x-y+4=0与
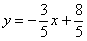 的交点?.
的交点?.由
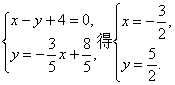
∴点P的坐标为
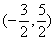 .
.可用两种方法来做,方法一:利用两点间的距离公式;方法二:垂直平分线

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
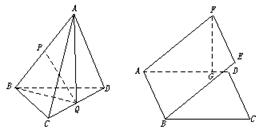
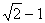
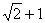
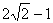
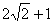
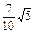 .
.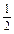 ;③P点到l1的距离与P点到l3的距离之比是
;③P点到l1的距离与P点到l3的距离之比是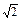 ∶
∶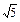 .若能,求P点坐标;若不能,说明理由.
.若能,求P点坐标;若不能,说明理由.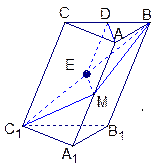
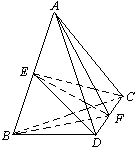
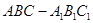 的各棱长均为2,侧棱
的各棱长均为2,侧棱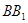 与底面
与底面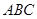 所成的角为
所成的角为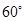 ,
,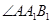 为锐角,且侧面
为锐角,且侧面 ⊥底面
⊥底面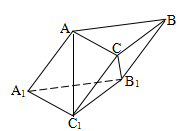
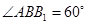 ;
;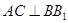 ;
;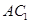 与平面
与平面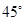 ;
;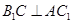 .
.