题目内容
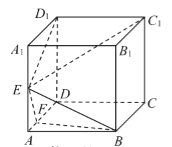
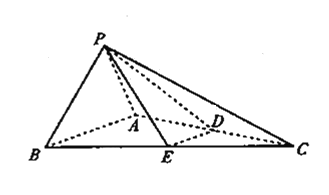
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,△DAB≌△DCB,E为线段BD上的点,且EA=EB=ED=AB,延长CE交AD于点F.
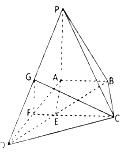
(1)若G为PD的中点,求证平面PAD⊥平面CGF;
(2)若AD=AP=6,求平面BCP与平面DCP所成锐二面角的余弦值.
【答案】(1)见解析(2)![]() .
.
【解析】
(1)推导出∠BCD=![]() ,EF⊥AD,AF=DF,GF⊥平面ABCD,GF⊥AD,从而AD⊥平面CFG,由此能证明平面PAD⊥平面CGF.
,EF⊥AD,AF=DF,GF⊥平面ABCD,GF⊥AD,从而AD⊥平面CFG,由此能证明平面PAD⊥平面CGF.
(2)以A为原点,AD为x轴,AB为y轴,AP为z轴,建立空间直角坐标系,利用向量法能求出平面BCP与平面DCP所成锐二面角的余弦值.
(1)证明:在△BCD中,EB=ED=EC=BC,∴∠BCD![]() ,
,
∵△DAB≌△DCB,∴△EAB≌△ECB,
∴∠FED=∠FEA=∠AEB![]() ,EC=EA,
,EC=EA,
∴∠FED=∠FEA,ED=EA,∴EF⊥AD,AF=DF,
∵PG=DG,∴FG∥PA,
∵PA⊥平面ABCD,∴GF⊥平面ABCD,∴GF⊥AD,
∵GF∩EF=F,∴AD⊥平面CFG,
∵AD平面PAD,∴平面PAD⊥平面CGF.
(2)解:由(1)知∠BCD![]() ,
,
∵△DAB≌△DCB,∴AB⊥AD,
∵AD=AP=6,![]() ,∴AB=2
,∴AB=2![]() ,
,
以A为原点,AD为x轴,AB为y轴,AP为z轴,建立空间直角坐标系,
P(0,0,6),B(0,2![]() ,0),C(3,3
,0),C(3,3![]() ,0),D(6,0,0),
,0),D(6,0,0),
![]() (0,2
(0,2![]() ,﹣6),
,﹣6),![]() (3,3
(3,3![]() ,﹣6),
,﹣6),![]() (6,0,﹣6),
(6,0,﹣6),
设平面BCP的法向量![]() (x,y,z),
(x,y,z),
则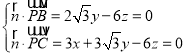 ,取x=1,得
,取x=1,得![]() (1,
(1,![]() ,﹣1),
,﹣1),
设平面DCP的法向量![]() (x,y,z),
(x,y,z),
则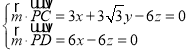 ,取x=1,得
,取x=1,得![]() (1,
(1,![]() ,1),
,1),
设平面BCP与平面DCP所成锐二面角的平面角为θ,
则cosθ .
.
∴平面BCP与平面DCP所成锐二面角的余弦值为![]() .
.