题目内容
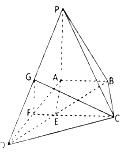
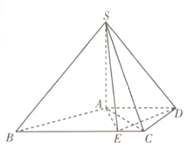
【题目】已知m,n是两条不同的直线,α,β是两个不同的平面,给出下列命题:
①若m∥n,n⊥β,mα,则α⊥β;
②若α⊥β,α∩β=m,n⊥m,则n⊥α或n⊥β;
③若m⊥α,m⊥n,nβ,则α∥β或α⊥β;
④若α∩β=m,n∥m,nα,nβ,则n∥α且n∥β;
其中正确命题的序号是( )
A.①②B.①③C.①④D.②④
【答案】C
【解析】
在①中,由面面垂直的判定定理得![]() ;在②中,
;在②中,![]() 有可能与
有可能与![]() ,
,![]() 都不垂直;在③中,
都不垂直;在③中,![]() 与
与![]() 有可能相交但不垂直;在④中,由线面平行的性质定理得
有可能相交但不垂直;在④中,由线面平行的性质定理得![]() 且
且![]() .
.
由![]() ,
,![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() 是两个不同的平面,知:
是两个不同的平面,知:
在①中,若![]() ,
,![]() ,
,![]() ,则由面面垂直的判定定理得
,则由面面垂直的判定定理得![]() ,故①正确;
,故①正确;
在②中,若![]() ,
,![]() ,
,![]() ,则
,则![]() 有可能与
有可能与![]() ,
,![]() 都不垂直,故②错误;
都不垂直,故②错误;
在③中,若![]() ,
,![]() ,
,![]() ,则
,则![]() 与
与![]() 相交或平行,即
相交或平行,即![]() 与
与![]() 有可能相交但不垂直,故③错误;
有可能相交但不垂直,故③错误;
在④中,若![]() ,
,![]() ,
,![]() ,
,![]() ,则由线面平行的性质定理得
,则由线面平行的性质定理得![]() 且
且![]() ,故④正确.
,故④正确.
故选:![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某学校在学期结束,为了解家长对学校工作的满意度,对两个班的100位家长进行满意度调查,调查结果如下:
非常满意 | 满意 | 合计 | |
A | 30 | 15 | 45 |
B | 45 | 10 | 55 |
合计 | 75 | 25 | 100 |
(1)根据表格判断是否有![]() 的把握认为家长的满意程度与所在班级有关系?
的把握认为家长的满意程度与所在班级有关系?
(2)用分层抽样的方法从非常满意的家长中抽取5人进行问卷调查,并在这5人中随机选出2人进行座谈,求这2人都来自同一班级的概率?
附:
|
|
|
|
|
|
|
|
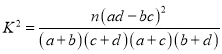
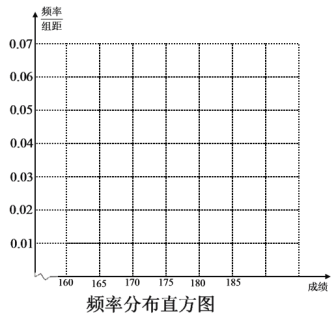
【题目】某美术学院2018年在山西招生,报名人数很多.工作人员在某个市区抽取了该区2018年美术招生考试成绩中200名学生的色彩和素描的初试成绩,按成绩分组,得到的频率分布表如下图所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 24 | 0.12 |
第2组 |
| ① | 0.18 |
第3组 |
| 64 | 0.32 |
第4组 |
| 60 | ② |
第5组 |
| 16 | 0.08 |
合计 | 200 | 1.00 | |
(1)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图,并由频率分布直方图估算中位数;
(2)为了能更清楚地了解该市学生的情况,该美院决定在复试以前先进行抽样调研.但受场地和教授人数的客观限制,决定从第3组选出3人,第4组选出2人,第5组选出1人,然后从这6人中再选出2人进行调研,求这2人均来自第三组的概率.