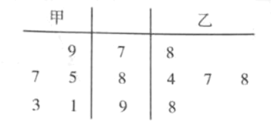
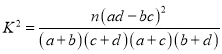题目内容
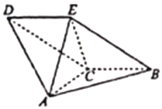
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E,F分别是棱AA1,AD上的点,且AE=EA1,AF![]() FD.
FD.
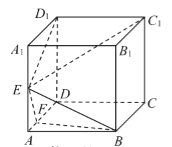
(1)求证:平面EC1D1⊥平面EFB;
(2)求二面角E﹣FB﹣A的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)以![]() 为坐标原点,以
为坐标原点,以![]() 为
为![]() 轴,
轴,![]() 为单位长,建立空间直角坐标系,利用向量法能证明平面
为单位长,建立空间直角坐标系,利用向量法能证明平面![]() 平面
平面![]() .
.
(2)求出平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,利用向量法能求出二面角
的法向量,利用向量法能求出二面角![]() 的余弦值.
的余弦值.
证明:(1)以![]() 为坐标原点,以
为坐标原点,以![]() 为
为![]() 轴,
轴,![]() 为单位长,建立如图所示的空间直角坐标系,
为单位长,建立如图所示的空间直角坐标系,
则![]() ,0,
,0,![]() ,
,![]() ,0,
,0,![]() ,
,![]() ,4,
,4,![]() ,
,![]() ,0,
,0,![]() ,
,![]() ,4,
,4,![]() ,
,
![]() ,4,
,4,![]() ,
,![]() ,0,
,0,![]() ,
,![]() ,0,
,0,![]() ,
,![]() ,4,
,4,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则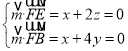 ,取
,取![]() ,得
,得![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则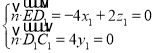 ,取
,取![]() ,得
,得![]() ,
,
![]()
![]() ,
,![]()
![]() ,
,
![]() 平面
平面![]() 平面
平面![]() .
.
解:(2)由题意得平面![]() 的法向量可取
的法向量可取![]() ,0,
,0,![]() ,
,
由(1)知平面![]() 的法向量
的法向量![]() ,
,![]() ,
,![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,
,
则![]() ,
,
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某学校在学期结束,为了解家长对学校工作的满意度,对两个班的100位家长进行满意度调查,调查结果如下:
非常满意 | 满意 | 合计 | |
A | 30 | 15 | 45 |
B | 45 | 10 | 55 |
合计 | 75 | 25 | 100 |
(1)根据表格判断是否有![]() 的把握认为家长的满意程度与所在班级有关系?
的把握认为家长的满意程度与所在班级有关系?
(2)用分层抽样的方法从非常满意的家长中抽取5人进行问卷调查,并在这5人中随机选出2人进行座谈,求这2人都来自同一班级的概率?
附:
|
|
|
|
|
|
|
|