题目内容
某抛物线型拱桥的跨度是20米,拱高4米.在建桥时每隔4米需要一支柱支撑,其中最长的支柱是多少米?
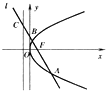
建立如图所示的直角坐标系,
设抛物线方程为x2=-2py(p>0),
∵过定点B(10,-4),
代入x2=-2py,得p=
.
∴x2=-25y.
当x=2时,y=
,
∴最长支柱长为4-|y|=4-
=3.84(m),
故在建桥时每隔4米需要一支柱支撑,其中最长的支柱是:3.84米.
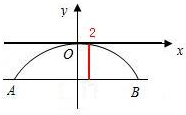
设抛物线方程为x2=-2py(p>0),
∵过定点B(10,-4),
代入x2=-2py,得p=
| 25 |
| 2 |
∴x2=-25y.
当x=2时,y=
| -4 |
| 25 |
∴最长支柱长为4-|y|=4-
| 4 |
| 25 |
故在建桥时每隔4米需要一支柱支撑,其中最长的支柱是:3.84米.


练习册系列答案
相关题目
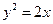 上的点
上的点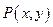 到点
到点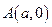
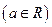 的距离的最小值记为
的距离的最小值记为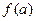 ,(1)求
,(1)求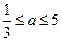 时,求
时,求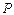 是抛物线
是抛物线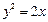 上的动点,点
上的动点,点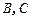 在
在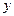 轴上,圆
轴上,圆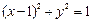 内切于
内切于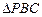 ,求
,求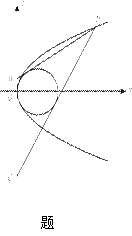
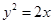 上的一个动点,则点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值为( )
上的一个动点,则点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值为( )