题目内容
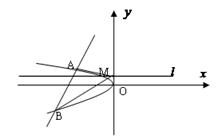
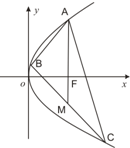
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B(|AF|>|BF|),交其准线于点C,若|BC|=2|BF|,且|AF|=2,则此抛物线的方程为______.
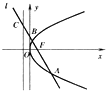

设A(x1,y1),B(x2,y2)
由抛物线的定义,得|AF|=
+x1=2,
∴x1=2-
∵直线l交抛物线准线于点C,|BC|=2|BF|,
∴x2=
,
由抛物线的性质,得x1x2=
(2-
)=
解之得p=1,可得此抛物线的方程为y2=2x
故答案为:y2=2x
由抛物线的定义,得|AF|=
| p |
| 2 |
∴x1=2-
| p |
| 2 |
∵直线l交抛物线准线于点C,|BC|=2|BF|,
∴x2=
| p |
| 6 |
由抛物线的性质,得x1x2=
| p |
| 6 |
| p |
| 2 |
| p2 |
| 4 |
解之得p=1,可得此抛物线的方程为y2=2x
故答案为:y2=2x

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是
是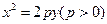 上的点,
上的点,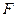 是抛物线的焦点,求证:
是抛物线的焦点,求证: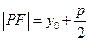 。
。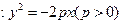 上横坐标为
上横坐标为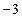 的一点,与其焦点的距离为4.(1)求
的一点,与其焦点的距离为4.(1)求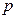 的值;(2)设动直线
的值;(2)设动直线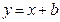 与抛物线C相交于A.B两点,问在直线
与抛物线C相交于A.B两点,问在直线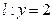 上是否存在与
上是否存在与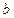 的取值无关的定点M,使得
的取值无关的定点M,使得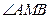 被直线
被直线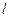 平分?若存在,求出点M的坐标;若不存在,说明理由.
平分?若存在,求出点M的坐标;若不存在,说明理由.