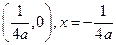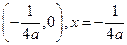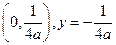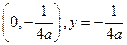题目内容
已知直线y=x+b与抛物线y2=2px(p>0)相交于A、B两点,若OA⊥OB,(O为坐标原点)且S△AOB=2
,求抛物线的方程.
| 5 |
设A(x1,y1)、B(x2,y2)
由
得x2-2(p-b)x+b2=0
则x1+x2=2(p-b),x1x2=b2
所以y1+y2=2p,y1y2=2pb
又因为OA⊥OB,
所以
•
=-1即
=
=-1
所以p=-
,所以x1+x2=-3b,y1+y2=-b,y1y2=-b2
又因为S△OAB=2
,|AB|=
b,原点O到AB的距离d=
所以
|AB|d=2
得b=±2,所以p=±1,
又因为p>0,所以p=1,y2=2x,
则抛物线的方程为y2=2x.
由
|
则x1+x2=2(p-b),x1x2=b2
所以y1+y2=2p,y1y2=2pb
又因为OA⊥OB,
所以
| y1 |
| x1 |
| y2 |
| x2 |
| 2pb |
| b2 |
| 2p |
| b |
所以p=-
| b |
| 2 |
又因为S△OAB=2
| 5 |
| 10 |
| |b| | ||
|
所以
| 1 |
| 2 |
| 5 |
又因为p>0,所以p=1,y2=2x,
则抛物线的方程为y2=2x.

练习册系列答案
相关题目
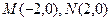 ,点
,点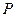 为坐标平面内的动点,且满足
为坐标平面内的动点,且满足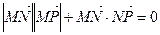 .
. 的方程;
的方程;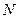 的直线
的直线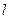 斜率为
斜率为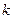 ,且与曲线
,且与曲线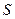 、
、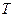 ,若
,若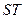 的垂直平分线交
的垂直平分线交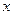 轴于
轴于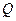 点,求
点,求
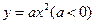 的焦点坐标和准线方程分别是( )
的焦点坐标和准线方程分别是( )