题目内容
已知M是抛物线y2=4x上的一点，F是抛物线的焦点，线段MF的中点P到y轴的距离为2，则|PF|=______．
依题意，设M在抛物线的准线x=-1上的射影为M′，线段MF的中点P在y轴上的射影为P′，在抛物线的准线x=-1上的射影为P″，作图如下：
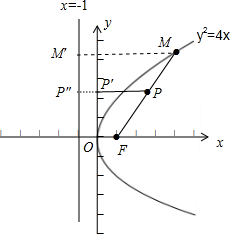
∵抛物线y2=4x的焦点F（1，0），准线方程为x=-1，设F在抛物线的准线上的射影为F′，则|FF′|=2；
依题意PP″为梯形FF′M′M的中位线，
∵|PP′|=2，
∴|PP″|=2-（-1）=3，
又|FF′|=2，
∴2|PP″|=|FF′|+|MM′|，即2×3=2+|MM′|，
∴|MM′|=4，又|MF|=|MM′|，
∴|MF|=4，又P为MF的中点，
∴|PF|=2．
故答案为：2．
∵抛物线y2=4x的焦点F（1，0），准线方程为x=-1，设F在抛物线的准线上的射影为F′，则|FF′|=2；
依题意PP″为梯形FF′M′M的中位线，
∵|PP′|=2，
∴|PP″|=2-（-1）=3，
又|FF′|=2，
∴2|PP″|=|FF′|+|MM′|，即2×3=2+|MM′|，
∴|MM′|=4，又|MF|=|MM′|，
∴|MF|=4，又P为MF的中点，
∴|PF|=2．
故答案为：2．
练习册系列答案
习题精选系列答案
相关题目
