题目内容
14.已知函数f(x)=xlnx-$\frac{a}{2}$x2(a∈R).(1)若a=2,求曲线y=f(x)在点[1,f(1)]处的切线方程;
(2)若函数g(x)=f(x)-x有两个极值点x1、x2,求证:$\frac{1}{ln{x}_{1}}$+$\frac{1}{ln{x}_{2}}$>2ae.
分析 (1)求出f(x)的导函数,切线斜率k=f′(1),利用切线的定义,即可求出切线方程;
(2)函数g(x)=f(x)-x有两个极值点x1、x2,即导函数g′(x)有两个不同的实数根x1、x2,对a进行分类讨论,令$t=\frac{{x}_{2}}{{x}_{1}}$>1,构造函数φ(t),利用函数φ(t)的单调性证明不等式.
解答 解:(1)当a=2时,f(x)=xlnx-x2,f′(x)=lnx+1-2x,
∴f(1)=-1,f′(1)=-1,
曲线y=f(x)在(1,f(1))处的切线方程为y=-x;
(2)g′(x)=f(x)′-1=lnx-ax,函数g(x)=f(x)-x有两个极值点x1、x2,
即g′(x)=lnx-ax=0有两个不同的实根,
当a≤0时,g′(x)单调递增,g′(x)=0不可能有两个不同的实根;
当a>0时,设h(x)=lnx-ax,${h}^{′}(x)=\frac{1-ax}{x}$,
若$0<x<\frac{1}{a}$时,h′(x)>0,h(x)单调递增,
若$x>\frac{1}{a}$时,h′(x)<0,h(x)单调递减,
∴$h(\frac{1}{a})=-lna-1$>0,∴0$<a<\frac{1}{e}$.
不妨设x2>x1>0,∵${g}^{′}({x}_{1})={g}^{′}({x}_{2})=0$,∴lnx1-ax1=0,lnx2-ax2=0,lnx1-lnx2=a(x1-x2),
先证$\frac{1}{ln{x}_{1}}+\frac{1}{ln{x}_{2}}>2$,即证$\frac{ln{x}_{2}-ln{x}_{1}}{{x}_{2}-{x}_{1}}<\frac{{x}_{1}+{x}_{2}}{2{x}_{1}{x}_{2}}$,
即证$ln\frac{{x}_{2}}{{x}_{1}}<\frac{{x}_{2}^{2}-{x}_{1}^{2}}{2{x}_{2}{x}_{1}}=\frac{1}{2}(\frac{{x}_{2}}{{x}_{1}}-\frac{{x}_{1}}{{x}_{2}})$
令$t=\frac{{x}_{2}}{{x}_{1}}>1$,即证$lnt<\frac{1}{2}(t-\frac{1}{t})$
设φ(t)=$lnt-\frac{1}{2}(t-\frac{1}{t})$,则φ′(t)=$\frac{2t-{t}^{2}-1}{2{t}^{2}}$=$\frac{-(t-1)^{2}}{2{t}^{2}}<0$
函数φ(t)在(1,+∞)上单调递减,∴φ(t)<φ(1)=0,∴证:$\frac{1}{ln{x}_{1}}$+$\frac{1}{ln{x}_{2}}$>2,
又∵ae<1,∴$\frac{1}{ln{x}_{1}}$+$\frac{1}{ln{x}_{2}}$>2ae.
点评 本题考查了,利用导数求函数的切线,运用分类讨论,等价转化思想证明不等式.是一道导数综合题,难题较大.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分条件 | D. | 既不充分也不必要条件 |
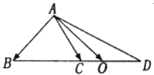 在△ABC中,点D在线段BC的延长线上,且$\overrightarrow{BC}$=$\overrightarrow{CD}$,点O在线段CD上(点O与点C,D不重合),若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x的取值范围是( )
在△ABC中,点D在线段BC的延长线上,且$\overrightarrow{BC}$=$\overrightarrow{CD}$,点O在线段CD上(点O与点C,D不重合),若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x的取值范围是( )| A. | (-1,0) | B. | (0,$\frac{1}{3}$) | C. | (0,1) | D. | (-$\frac{1}{3}$,0) |