题目内容
5.已知抛物线C1:y2=2px(p>0)的准线截圆C2:x2+y2=1所得的弦长为$\sqrt{3}$.(1)求抛物线C1 的方程;
(2)倾斜角为$\frac{π}{4}$且经过点(2,0)的直线l与抛物线C1相交于A、B两点,求证:OA⊥OB.
分析 (1)利用弦心距、半弦长与半径之间的关系计算即得结论;
(2)通过设直线l的方程并与抛物线方程联立,利用韦达定理及向量数量积计算即得结论.
解答 (1)解:∵抛物线C1的直线方程为:x=-$\frac{p}{2}$,
∴圆心(0,0)到其距离为$\frac{p}{2}$,
由已知得2$\sqrt{{1}^{2}-(\frac{p}{2})^{2}}$=$\sqrt{3}$,解得p=1,
∴抛物线C1 的方程为:y2=2x;
(2)证明:直线l的方程为:y=x-2,
联立$\left\{\begin{array}{l}{{y}^{2}=2x}\\{y=x-2}\end{array}\right.$,消去y得:x2-6x+4=0,
设A(x1,y1),B(x2,y2),
由韦达定理知:x1+x2=6,x1x2=4,
∵$\overrightarrow{OA}•\overrightarrow{OB}$=(x1,y1)•(x2,y2)
=x1x2+(x1-2)(x2-2)
=2x1x2-2(x1+x2)+4
=2×4-2×6+4=0,
∴OA⊥OB.
点评 本题考查求抛物线方程,考查直线与直线的垂直关系,注意解题方法的积累,属于中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
3.已知点A的坐标为(4$\sqrt{3}$,1),将OA绕坐标原点O逆时针旋转$\frac{π}{3}$至OB,则点B的纵坐标为( )
| A. | $\frac{{3\sqrt{3}}}{2}$ | B. | $\frac{{5\sqrt{3}}}{2}$ | C. | $\frac{11}{2}$ | D. | $\frac{13}{2}$ |
10.设 Pn(xn,yn)是直线2x-y=$\frac{n}{n+1}$(n∈N*)与圆x2+y2=2在第一象限的交点,则极限$\lim_{n→∞}\frac{{{y_n}-1}}{{{x_n}-1}}$=( )
| A. | -1 | B. | -$\frac{1}{2}$ | C. | 1 | D. | 2 |
10.定义运算“•”如下:x•y=$\left\{\begin{array}{l}{x,x≥y}\\{y,x<y}\end{array}\right.$,若函数f(x)=m-(1-2x)•(2x-2)有两个零点,则( )
| A. | m∈(-$\frac{1}{2}$,+∞) | B. | m∈(-$\frac{1}{2}$,1) | C. | m∈[-$\frac{1}{2}$,+∞) | D. | m∈[-$\frac{1}{2}$,1) |
17.以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.已知直线l的参数方程为$\left\{\begin{array}{l}x=3-t\\ y=t-5\end{array}\right.$(t为参数),圆C的极坐标方程为ρ=4(cosθ+sinθ),则圆C上的点到直线l的距离的最大值为( )
| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 5$\sqrt{2}$ |
15.已知a>0且a≠1,命题“?x>1,logax>0”的否定是( )
| A. | ?x≤1,logax>0 | B. | ?x>1,loga≤0 | C. | ?x≤1,logax>0 | D. | ?x>1,logax≤0 |
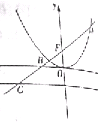 如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=$\sqrt{2}$|BF|,且|AF|=4+2$\sqrt{2}$,则p=2.
如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=$\sqrt{2}$|BF|,且|AF|=4+2$\sqrt{2}$,则p=2.