题目内容

2．二项式（x+y）6的展开式中，含x4y2的项的系数是15．

分析 写出二项展开式的通项，取r=2即可求得含x4y2的项的系数．

解答 解：由${T}_{r+1}={C}_{6}^{r}{x}^{6-r}{y}^{r}$，令r=2，
可得二项式（x+y）6的展开式中，含x4y2的项的系数是${C}_{6}^{2}=15$．
故答案为：15．

点评 本题考查了二项式系数的性质，关键是熟记二项展开式的通项，是基础题．

练习册系列答案
相关题目
12．函数y=cos（2x+$\frac{π}{6}$）的图象可由函数y=sin2x的图象（　　）
A．向左平移$\frac{π}{3}$个单位而得到B．向右平移$\frac{π}{3}$个单位而得到
C．向左平移$\frac{π}{6}$个单位而得到D．向右平移$\frac{π}{6}$个单位而得到
13．已知集合A={-1，1，3}，B={2，2a-1}，A∩B={1}，则实数a的值是1．
10．执行如图所示的程序框图，若输出的y=$\frac{1}{2}$，则输入的x的值可能为（　　）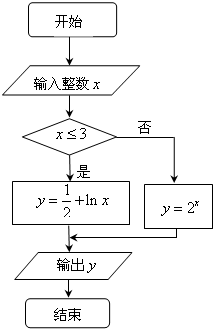
A．-1B．0C．1D．5
17．已知$\frac{a+3i}{i}$=b+i（a，b∈R，i为虚数单位），则a+b等于（　　）
A．-4B．-2C．2D．4
7．已知数列{an}满足a1=4，a2=2，an+2=$\frac{3+（-1）^{n}}{2}$an+2[1-（-1）n]，n∈N*，k∈N*．
（Ⅰ）求a3，a4，并直接写出an；
（Ⅱ）设Sk=a1+a3+…+a2k-1，Tk=a2+a4+…+a2k，分别求Sk，Tk关于k的表达式；
（Ⅲ）设Wk=$\frac{{2{S_k}}}{{2+{T_k}}}$，求使Wk＞2的所有k的值，并说明理由．
14．若x（xlnx）′=lnx+1，a=${∫}_{1}^{e}$lnxdx，a100+2C${\;}_{100}^{1}$a99+22C${\;}_{100}^{2}$a98+…+299C${\;}_{100}^{1}$a+2100被10除得的余数为（　　）
A．3B．1C．9D．7
11．三个正数成等比数列，它们的和等于21，倒数的和等于$\frac{7}{12}$，求这三个数．
12．已知集合A={x|y=$\sqrt{1-{x}^{2}}$，x∈z}，B={p-q|p∈A，q∈A}，则B中元素个数为（　　）
A．1B．3C．5D．7

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网