题目内容
(本小题满分16分)
如图,已知抛物线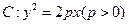 的焦点为
的焦点为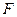 ,
,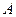 是抛物线上横坐标为8且位于
是抛物线上横坐标为8且位于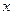 轴上方的点.
轴上方的点. 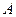 到抛物线准线的距离等于10,过
到抛物线准线的距离等于10,过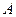 作
作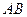 垂直于
垂直于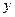 轴,垂足为
轴,垂足为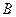 ,
,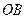 的中点为
的中点为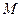 (
(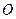 为坐标原点).
为坐标原点).
(Ⅰ)求抛物线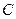 的方程;
的方程;
(Ⅱ)过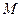 作
作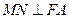 ,垂足为
,垂足为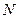 ,求点
,求点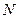 的坐标;
的坐标;
(Ⅲ)以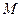 为圆心,4为半径作圆
为圆心,4为半径作圆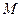 ,点
,点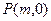 是
是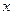 轴上的一个动点,试讨论直线
轴上的一个动点,试讨论直线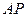 与圆
与圆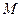 的位置关系.
的位置关系.

如图,已知抛物线
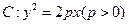 的焦点为
的焦点为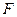 ,
,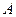 是抛物线上横坐标为8且位于
是抛物线上横坐标为8且位于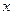 轴上方的点.
轴上方的点. 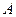 到抛物线准线的距离等于10,过
到抛物线准线的距离等于10,过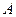 作
作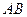 垂直于
垂直于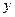 轴,垂足为
轴,垂足为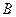 ,
,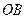 的中点为
的中点为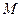 (
(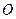 为坐标原点).
为坐标原点).
(Ⅰ)求抛物线
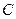 的方程;
的方程;(Ⅱ)过
 作
作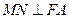 ,垂足为
,垂足为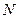 ,求点
,求点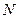 的坐标;
的坐标;(Ⅲ)以
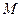 为圆心,4为半径作圆
为圆心,4为半径作圆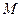 ,点
,点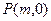 是
是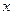 轴上的一个动点,试讨论直线
轴上的一个动点,试讨论直线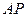 与圆
与圆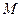 的位置关系.
的位置关系.
(Ⅰ)
(Ⅱ)
(Ⅲ)当 时,直线AP与圆M相离,当m=2时,直线AP与圆M相切;
时,直线AP与圆M相离,当m=2时,直线AP与圆M相切;
当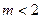 时,直线AP与圆M相交。
时,直线AP与圆M相交。

(Ⅱ)

(Ⅲ)当
 时,直线AP与圆M相离,当m=2时,直线AP与圆M相切;
时,直线AP与圆M相离,当m=2时,直线AP与圆M相切;当
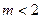 时,直线AP与圆M相交。
时,直线AP与圆M相交。解:(I)抛物线的准线为
 ………………4分
………………4分
(II)
又 ………………6分
………………6分


则直线FA的方程为 …………8分
…………8分
联立方程组,解得
 ………………10分
………………10分
 (III)由题意得,圆M的圆心坐标为(0,4),半径为4
(III)由题意得,圆M的圆心坐标为(0,4),半径为4
当m=8时,直线AP的方程为 ,此时,直线AP与圆M相离 …………12分
,此时,直线AP与圆M相离 …………12分
当 时,直线AP的方程为
时,直线AP的方程为 ,
,
即为 ,所以圆M(0,4)到直线AP的距离
,所以圆M(0,4)到直线AP的距离

令 ………………14分
………………14分
综上所述,当 时,直线AP与圆M相离,当m=2时,直线AP与圆M相切;
时,直线AP与圆M相离,当m=2时,直线AP与圆M相切;
当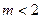 时,直线AP与圆M相交 ………………16分
时,直线AP与圆M相交 ………………16分
(说明:“当m=8”时这种情形没有列出,扣2分)

 ………………4分
………………4分(II)

又
 ………………6分
………………6分

则直线FA的方程为
 …………8分
…………8分联立方程组,解得
 ………………10分
………………10分 (III)由题意得,圆M的圆心坐标为(0,4),半径为4
(III)由题意得,圆M的圆心坐标为(0,4),半径为4当m=8时,直线AP的方程为
 ,此时,直线AP与圆M相离 …………12分
,此时,直线AP与圆M相离 …………12分当
 时,直线AP的方程为
时,直线AP的方程为 ,
,即为
 ,所以圆M(0,4)到直线AP的距离
,所以圆M(0,4)到直线AP的距离
令
 ………………14分
………………14分综上所述,当
 时,直线AP与圆M相离,当m=2时,直线AP与圆M相切;
时,直线AP与圆M相离,当m=2时,直线AP与圆M相切;当
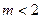 时,直线AP与圆M相交 ………………16分
时,直线AP与圆M相交 ………………16分(说明:“当m=8”时这种情形没有列出,扣2分)

练习册系列答案
相关题目
 . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”. .求证:
.求证: 为曲线
为曲线 的“上夹线”.
的“上夹线”. 

 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明. ,点
,点 满足
满足 ,记点
,记点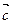 ="(1,1)" 的直线l与点P的轨迹交于A,B两点,当
="(1,1)" 的直线l与点P的轨迹交于A,B两点,当 时,求
时,求 AOB的面积。(9分)
AOB的面积。(9分)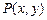 到点
到点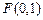 与到直线
与到直线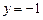 的距离相等,求点
的距离相等,求点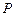 的轨迹
的轨迹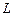 的方程;
的方程; 的三个顶点
的三个顶点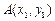 ,
,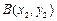 ,
,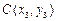 (
(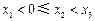 )在(Ⅰ)中的曲线
)在(Ⅰ)中的曲线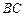 的斜率为
的斜率为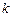 ,
,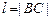 ,求
,求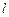 关于
关于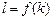 ;
;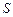 的最小值。
的最小值。 .
. 时,求
时,求 的最大、最小值.
的最大、最小值.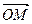 ·
· =0,其中点
=0,其中点
 过点
过点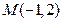 且与直线
且与直线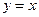 垂直,抛物线C:
垂直,抛物线C: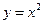 与直线
与直线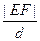 的最大值.并求出此时b的值
的最大值.并求出此时b的值 和圆
和圆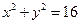 交于
交于 两点,则
两点,则 的中点坐
的中点坐






