题目内容
设直线 . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.
⑴已知函数 .求证:
.求证: 为曲线
为曲线 的“上夹线”.
的“上夹线”.
⑵观察下图:


根据上图,试推测曲线 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.
 . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.⑴已知函数
 .求证:
.求证: 为曲线
为曲线 的“上夹线”.
的“上夹线”. ⑵观察下图:


根据上图,试推测曲线
 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.(1)见解析(2)见解析
⑴由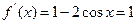 得
得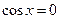 ,当
,当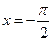 时,
时,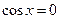 ,
,
此时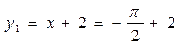 ,
,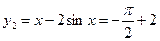 ,
,
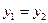 ,所以
,所以 是直线
是直线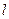 与曲线
与曲线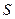 的一个切点;
的一个切点;
当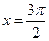 时,
时,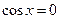 ,此时
,此时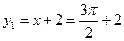 ,
,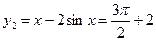 ,
,
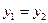 ,所以
,所以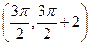 是直线
是直线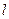 与曲线
与曲线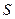 的一个切点;
的一个切点;
所以直线l与曲线S相切且至少有两个切点;
对任意x∈R,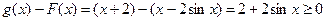 ,所以
,所以
因此直线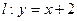 是曲线
是曲线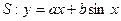 的“上夹线”.(6分)
的“上夹线”.(6分)
⑵推测: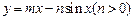 的“上夹线”的方程为
的“上夹线”的方程为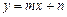
①先检验直线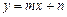 与曲线
与曲线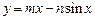 相切,且至少有两个切点:设:
相切,且至少有两个切点:设: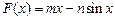
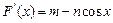 ,
, 令
令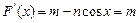 ,得:
,得: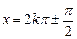 (k
(k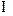 Z)
Z)
当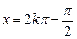 时,
时,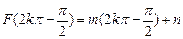
故:过曲线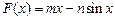 上的点(
上的点(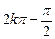 ,
,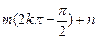 )的切线方程为:
)的切线方程为:
y-[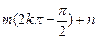 ]=
]=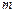 [
[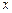 -(
-(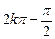 )],化简得:
)],化简得: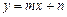 .
.
即直线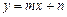 与曲线
与曲线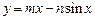 相切且有无数个切点.不妨设
相切且有无数个切点.不妨设
②下面检验g(x)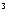 F(x)
F(x) 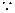 g(x)-F(x)=
g(x)-F(x)= 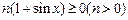
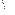 直线
直线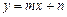 是曲线
是曲线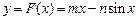 的“上夹线”. (13分)
的“上夹线”. (13分)
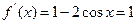 得
得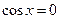 ,当
,当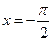 时,
时,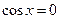 ,
,此时
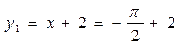 ,
,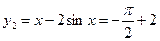 ,
, 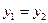 ,所以
,所以 是直线
是直线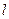 与曲线
与曲线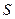 的一个切点;
的一个切点; 当
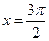 时,
时,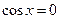 ,此时
,此时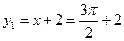 ,
,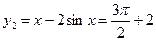 ,
, 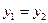 ,所以
,所以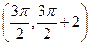 是直线
是直线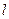 与曲线
与曲线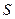 的一个切点;
的一个切点; 所以直线l与曲线S相切且至少有两个切点;
对任意x∈R,
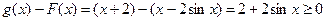 ,所以
,所以
因此直线
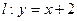 是曲线
是曲线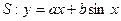 的“上夹线”.(6分)
的“上夹线”.(6分)⑵推测:
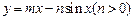 的“上夹线”的方程为
的“上夹线”的方程为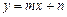
①先检验直线
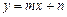 与曲线
与曲线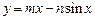 相切,且至少有两个切点:设:
相切,且至少有两个切点:设: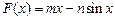
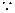
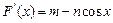 ,
,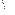 令
令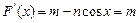 ,得:
,得: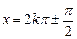 (k
(k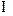 Z)
Z) 当
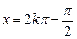 时,
时,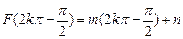
故:过曲线
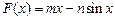 上的点(
上的点(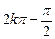 ,
,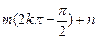 )的切线方程为:
)的切线方程为:y-[
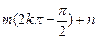 ]=
]=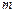 [
[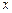 -(
-(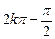 )],化简得:
)],化简得: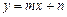 .
.即直线
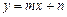 与曲线
与曲线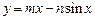 相切且有无数个切点.不妨设
相切且有无数个切点.不妨设
②下面检验g(x)
 F(x)
F(x)  g(x)-F(x)=
g(x)-F(x)= 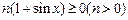
 直线
直线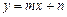 是曲线
是曲线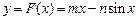 的“上夹线”. (13分)
的“上夹线”. (13分)
练习册系列答案
相关题目
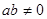 ,则方程
,则方程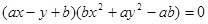 表示的曲线只可能是
表示的曲线只可能是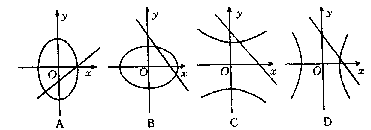
 =
= ,设点P的轨迹为曲线C,定点为M(4
,设点P的轨迹为曲线C,定点为M(4 ,0),直线PM交曲线C于另外一点Q.(1)求曲线C的方程;(2)求△OPQ面
,0),直线PM交曲线C于另外一点Q.(1)求曲线C的方程;(2)求△OPQ面 最大值.
最大值.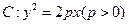 的焦点为
的焦点为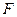 ,
,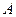 是抛物线上横坐标为8且位于
是抛物线上横坐标为8且位于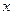 轴上方的点.
轴上方的点. 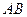 垂直于
垂直于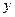 轴,垂足为
轴,垂足为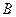 ,
,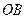 的中点为
的中点为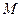 (
(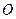 为坐标原点).
为坐标原点).
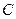 的方程;
的方程;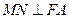 ,垂足为
,垂足为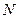 ,求点
,求点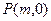 是
是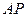 与圆
与圆
 ,(
,( )的一个焦点,且这条准线与双曲线的两个焦点连线互相垂直,又抛 物线与双曲线交于点
)的一个焦点,且这条准线与双曲线的两个焦点连线互相垂直,又抛 物线与双曲线交于点 ,求抛物线和双曲线的方程.
,求抛物线和双曲线的方程. :
: 过抛物线
过抛物线 的焦点.
的焦点. ,若
,若 ,直线
,直线 :
: ,
, 为平面上的动点,过点
为平面上的动点,过点 ,且
,且 .
. 的方程;
的方程; 过定点
过定点 ,圆心
,圆心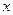 轴交于
轴交于 、
、 两点,设
两点,设 ,
, ,求
,求 的最大值.
的最大值. 关于直线
关于直线 对称的曲线方程是( )
对称的曲线方程是( )



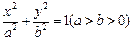 与抛物线
与抛物线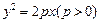 有相同的焦点
有相同的焦点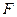 ,
,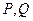 是椭圆与抛物线的的交点,若
是椭圆与抛物线的的交点,若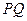 经过焦点
经过焦点