题目内容
【题目】如图,四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,底面
,底面![]() 为梯形,
为梯形,![]() ,
,![]() ,
,![]() ,且
,且![]() 与
与![]() 均为正三角形,
均为正三角形,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 重心.
重心.

(1)求证:![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
【答案】(Ⅰ)详见解析(Ⅱ)![]()
【解析】
试题分析: (Ⅰ)连接![]() 与
与![]() 交于
交于![]() ,连接
,连接![]() .在梯形
.在梯形![]() 中,根据两平行边的比例,可得
中,根据两平行边的比例,可得![]() 的比值,在
的比值,在![]() 中,由重心的性质,可得
中,由重心的性质,可得![]() 间的比值,两比值相等,则
间的比值,两比值相等,则![]() ,再由线线平行去证明线面平行; (Ⅱ)根据所给条件可证
,再由线线平行去证明线面平行; (Ⅱ)根据所给条件可证![]() ,且求出
,且求出![]() 的长.由
的长.由![]() ,可将所求三棱锥
,可将所求三棱锥![]() 的体转化为求三棱锥
的体转化为求三棱锥![]() 体积,再转化为三棱锥
体积,再转化为三棱锥![]() 体积,又
体积,又![]() ,只需求
,只需求![]() 即可.
即可.
试题解析:(Ⅰ)方法一:连![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
由梯形![]() ,
,![]() 且
且![]() ,知
,知![]()
又![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的重心,∴
的重心,∴![]()
在![]() 中,
中,![]() ,故
,故![]() //
//![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() //平面
//平面![]() .
.
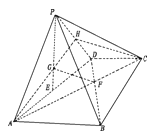
方法二:过![]() 作
作![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
![]()
![]() 为
为![]() 的重心,
的重心,![]() ,
,![]() ,
,
又![]() 为梯形,
为梯形,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ∴
∴![]()
又由所作![]() ,
,![]() 得
得![]() //
//![]() ,
,![]() 为平行四边形.
为平行四边形.
![]() ,
,![]()
![]() 面
面![]()

方法三:过![]() 作
作![]() //
//![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
由![]() 为正三角形,
为正三角形, ![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 重心,
重心,
得![]() ,
,![]()
又由梯形![]() ,
,![]() ,且
,且![]() ,
,
知![]() ,即
,即![]()
∴在![]() 中,
中,![]() //
//![]() ,所以平面
,所以平面![]() //平面
//平面![]()
又![]() 平面
平面![]() ,∴
,∴![]() 面
面![]()
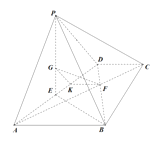
(Ⅱ) 方法一:由平面![]() 平面
平面![]() ,
,![]() 与
与![]() 均为正三角形,
均为正三角形,![]() 为
为![]() 的中点
的中点
∴![]() ,
,![]() ,得
,得![]() 平面
平面![]() ,且
,且![]()
由(Ⅰ)知![]() //平面
//平面![]() ,∴
,∴![]()
又由梯形![]() ,
,![]() ,且
,且![]() ,知
,知![]()
又![]() 为正三角形,得
为正三角形,得![]() ,∴
,∴![]() ,
,
得![]()
∴三棱锥![]() 的体积为
的体积为![]() .
.
方法二: 由平面![]() 平面
平面![]() ,
,![]() 与
与![]() 均为正三角形,
均为正三角形,![]() 为
为![]() 的中点
的中点
∴![]() ,
,![]() ,得
,得![]() 平面
平面![]() ,且
,且![]()
由![]() ,∴
,∴![]()
而又![]() 为正三角形,得
为正三角形,得![]() ,得
,得![]() .
.
∴![]() ,∴三棱锥
,∴三棱锥![]() 的体积为
的体积为![]() .
.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目