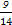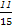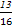题目内容
已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数),且a2=4,a6=8a3.
(1)求an;
(2)求数列{nan}的前n项和Tn.
(1)求an;
(2)求数列{nan}的前n项和Tn.
(1) an=2n (2) Tn=(n-1)2n+1+2
解:(1)由Sn=kcn-k,
得an=Sn-Sn-1=kcn-kcn-1(n≥2),
由a2=4,a6=8a3,
得kc(c-1)=4,kc5(c-1)=8kc2(c-1),
解得
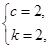
所以a1=S1=2,an=kcn-kcn-1=2n(n≥2),
于是an=2n.
(2)Tn=
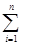 iai=
iai=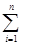 i·2i,
i·2i,即Tn=2+2·22+3·23+4·24+…+n·2n,
Tn=2Tn-Tn=-2-22-23-24-…-2n+n·2n+1
=-2n+1+2+n·2n+1
=(n-1)2n+1+2.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 <2.
<2.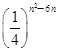 (n∈N*),bn=log2an,则数列{bn}的前n项和Sn取最大时,n=________.
(n∈N*),bn=log2an,则数列{bn}的前n项和Sn取最大时,n=________.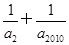 的最小值为________.
的最小值为________.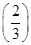 n}中的最大项是第k项,则k= .
n}中的最大项是第k项,则k= .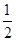
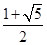
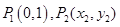 ,……,
,……,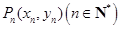 .若点
.若点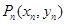 到点
到点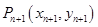 的变化关系为:
的变化关系为: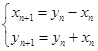
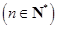 ,则
,则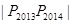 等于 .
等于 .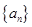 中,已知
中,已知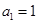 ,
,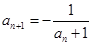 ,记
,记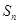 为数列
为数列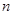 项和,则
项和,则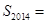 .
.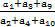 =( )
=( )