题目内容
20.已知函数f(x)=$\left\{\begin{array}{l}{\sqrt{x-1}\\;x>1}\\{x-1\\;x≤1}\end{array}\right.$,g(x)=$\left\{\begin{array}{l}{1-x\\;x>-1}\\{\sqrt{1-x}\\;x≤-1}\end{array}\right.$,F(x)=f(x)+g(x).(1)求F(3),F(-3);
(2)求F(x)的表达式.
分析 (1)直接代入计算,求F(3),F(-3);
(2)分类讨论,即可求F(x)的表达式.
解答 解:(1)F(3)=f(3)+g(3)=$\sqrt{2}$-2;F(-3)=f(-3)+g(-3)=-4+2=-2;
(2)x≤-1时,F(x)=x-1+$\sqrt{1-x}$,
-1<x≤1时,F(x)=x-1+1-x=0,
x>1时,F(x)=$\sqrt{x-1}$+1-x,
∴F(x)=$\left\{\begin{array}{l}{x-1+\sqrt{1-x},x≤-1}\\{0,-1<x≤1}\\{\sqrt{x-1}+1-x,x>1}\end{array}\right.$.
点评 本题考查函数的解析式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
8.函数f(x)=Asin(wx+φ)(A>0,w>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{3π}{2}$)的值是( )
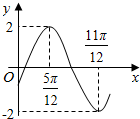

| A. | -1 | B. | 1 | C. | -$\sqrt{3}$ | D. | $\sqrt{3}$ |
5.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(2,m2),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则 m的值为( )
| A. | 2或-1 | B. | -2或1 | C. | ±2 | D. | ±1 |
6.f(x)为奇函数,且在(-∞,0)为递增,f(-2)=0,则xf(x)>0的解集为( )
| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-2,0)∪(0,2) | D. | (-2,0)∪(2,+∞) |